Числа от 1 до 1000
Деление на двузначное и трёхзначное число
Письменное деление на двузначное число
Ответы к стр. 58
При делении с остатком на двузначное число рассуждают также, как и при делении без остатка. Объясни, как выполнено деление с остатком.
_ 324 |62 _ 526 |74 _ 793 |83
310 |5 518 |7 474 |9
14 8 46
Надо 324 разделить на 62.
Разделю 324 не на 62, а на 60, чтобы легче было найти цифру частного. Для этого разделю 32 на 6, получу 5. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 5.
Умножу 62 на 5, получится 310. Вычту: 324 — 310 = 14, 14 меньше 62, значит, цифра 5 подходит, а 14 — остаток. Теперь её можно записать в частном.
Надо 526 разделить на 74.
Разделю 526 не на 74, а на 70, чтобы легче было найти цифру частного. Для этого разделю 52 на 7, получу 7. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 7.
Умножу 74 на 7, получится 518. Вычту: 526 — 518 = 8, 8 меньше 74, значит, цифра 7 подходит, а 8 — остаток. Теперь её можно записать в частном.
Надо 793 разделить на 83.
Разделю 793 не на 83, а на 80, чтобы легче было найти цифру частного. Для этого разделю 79 на 8, получу 9. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 9.
Умножу 83 на 9, получится 747. Вычту: 793 — 747 = 46, 46 меньше 83, значит, цифра 9 подходит, а 46 — остаток. Теперь её можно записать в частном.
211. Найди частное и остаток, проверь решение.
156 : 48 278 : 62 346 : 56 445 : 73
— 156 |48 Проверка:
144 |3 × 48
12 3
144
144 + 12 = 156
— 278 |62 Проверка:
248 |4 × 62
30 4
248
248 + 30 = 278
— 346 |56 Проверка:
336 |6 × 56
10 6
336
336 + 10 = 346
— 445 |73 Проверка:
438 |6 × 73
7 6
438
438 + 7 = 445
212. Космонавты были в полёте 290 ч. Сколько это суток и часов?
1 сутки = 24 часа
— 290 |24
24 |12 — суток
_50
48
2 — часа
О т в е т: 12 суток и 2 часа.
213. Площадь первого участка 120 м2, второго 160 м2. При одинаковой норме высева на 1 м2 на первом участке высеяли семян ржи на 1 кг меньше, чем на втором. Объясни, что означают выражения.
160 — 120 1000 : (160 — 120) 1000 : (160 — 120) • 160
160 — 120 — разница между площадями участков
1000 : (160 — 120) — столько грамм семян высеяли на 1 м2
1000 : (160 – 120) • 160 – столько грамм семян высеяли на втором участке
214. В международном автопробеге участвовало 350 машин. Экипаж каждой машины состоял из трёх спортсменов. До финиша не дошли 105 машин. Сколько машин и сколько спортсменов прибыли к финишу?
1) 350 – 105 = 245 (м.) — дошли до финиша
2) 245 • 3 = 735 (с.) — прибыли к финишу
О т в е т: 245 машин и 735 спортсменов.
215. Составь по задачам уравнения и реши их.
1) Какое число надо уменьшить на 28, чтобы получить число, равное сумме чисел 58 и 37?
2) Какое число надо увеличить в 8 раз, чтобы получить число, равное произведению чисел 80 и 12?
3) Какое число надо уменьшить в 28 раз, чтобы получить число, равное разности чисел 300 и 203?
1) x — 28 = 58 + 37
x — 28 = 95
x = 95 + 28
x = 123
2) x • 8 = 80 • 12
x • 8 = 960
x = 960 : 8
x = 120
3) x : 28 = 300 — 203
x : 28 = 97
x = 97 • 28
x = 2716
216. 384 : 96 192 : 48 648 : 72 352 • 46 — 5840 : 80
— 384 |96 — 192 |48
384 |4 192 |4
0 0
— 648 |72
648 |9
0
352 • 46 — 5840 : 80 = 16192 — 73 = 16119
× 352 — 5840|80
46 560 |73
+ 2112 —240
1408 240
16192 0
_16192
73
16119
217. Найди значения выражений 360 : с и 360 • с, если с = 1; c = 3; c = 4; c = 6; c = 10.
Наблюдай, как при этом изменяется частное, как изменяется произведение.
360 : 1 = 360 360 • 1 = 360
360 : 3 = 120 360 • 3 = 1080
360 : 4 = 90 360 • 4 = 1440
360 : 6 = 60 360 • 6 = 2160
360 : 10 = 36 360 • 10 = 3600
Значение частного уменьшается, а значение произведения увеличивается.
218. Выложи из палочек такую фигуру. Какие углы в этой фигуре? Переложи 4 палочки так, чтобы получилось два остроугольных треугольника. Будут ли эти треугольники равнобедренными? равносторонними?
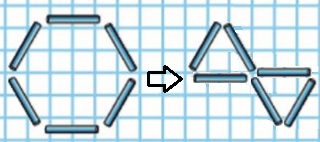
В этой фигуре все углы тупые.
Эти треугольники будут и равнобедренными и равносторонними. Равнобедренный треугольник — это треугольник, у которого две стороны равны по длине. Условие равенства двух сторон является необходимым и достаточным, чтобы считать треугольник равнобедренным. Это условие в равностороннем треугольнике выполняется всегда. Следовательно равносторонний треугольник всегда является равнобедренным.
399 : 57 236 : 59 475 : 95 609 • 27 — 4320 : 60
— 399 |57 — 236 |59
399 |7 236 |4
0 0
— 475 |95
475 |5
0
609 • 27 — 4320 : 60 = 16443 — 72 = 16371
× 609 — 4320|60
27 420 |72
+ 4263 —120
1218 120
16443 0
_16443
72
16371
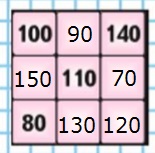
ЗАДАНИЕ НА ПОЛЯХ
МАГИЧЕСКИЙ КВАДРАТ
| ← Предыдущая | Следующая → |