Измерение величин
Многоугольники
Ответы к стр. 127
565. а) Какую линию называют ломаной линией?
б) Что называют звеньями ломаной?
в) Как обозначают ломаную?
г) Какую ломаную называют замкнутой?
а) Ломаной линией называют несколько точек на плоскости, соединенных отрезками, если никакие два из этих отрезков, имеющих общие точки, не лежат на одной прямой.
б) Отрезки, соединяющие точки ломаной, называют звеньями ломаной.
в) Ломаную обозначают, обозначив ее точки заглавными латинскими буквами.
г) Если конец ломаной совпадает с ее началом, то ломаную называют замкнутой, а фигуру, образованную этой замкнутой ломаной — многоугольником.
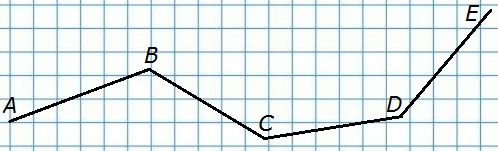
566. Постройте ломаную ABCDE. Назовите все её звенья.
Звенья: AB, BC, CD, DE.
567. Существует ли замкнутая ломаная, имеющая три звена, длины которых равны:
а) 1 см, 2 см, 2 см; б) 1 см, 2 см, 3 см; в) 1 см, 2 см, 4 см?
Во всех случаях звена всего три, следовательно, замкнутая ломаная будет треугольником. Треугольник можно построить, если сумма длин двух меньших сторон будет больше длины третьей стороны.
а) 2 < 2 + 1 — замкнутая ломаная, имеющая три звена, длины которых равны 1 см, 2 см, 2 см существует;
б) 3 = 1 + 2 — замкнутая ломаная, имеющая три звена, длины которых равны 1 см, 2 см, 3 см не существует.
в) 4 > 1 + 2 — замкнутая ломаная, имеющая три звена, длины которых равны 1 см, 2 см, 4 см не существует.
568. На рисунке 117 изображена ломаная ABCD. AB = 3 см, BC = 4 см, CD = 13 см, AD = 12 см. Определите длину ломаной ABCD и расстояние между ее концами.

1) ABCD = AB + BC + CD = 3 см + 4 см + 13 см = 20 см − длина ломаной
2) AD = 12 см − расстояние между ее концами
О т в е т: длина ломаной 20 см, расстояние между ее концами 12 см.
Доказываем
569. Докажите, что длина ломаной ABC больше длины ломаной ADC (рис. 118).

ABC = AB + BC, ADC = AD + DC.
Нужно доказать, что:
AD + DC < AB + BC.
Прибавим к обеим ломаным отрезок DE:
AB + BC + DE;
AD + DC + DE.
AD + DE = AE;
BE + EC = BC, значит:
AB + BC + DE и AE + DC.
В треугольнике длина каждой стороны меньше суммы длин двух других сторон, поэтому:
AE < AB + BE, a DC < EC + DE, значит:
AE + DC < (AB + BE) + (EC + DE).
AE = AD + DE, а BC = BE + EC, поэтому:
AD + DE + DC < AB + BC + DE.
Теперь вычтем DE:
AD + DC < AB + BC, что и требовалось доказать.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.