Измерение величин
Многоугольники
Ответы к стр. 128
570. а) Что называют многоугольником?
б) Что называют сторонами, углами, вершинами многоугольника?
в) Что называют периметром многоугольника?
г) Какой многоугольник называют выпуклым?
д) Какие многоугольники называют равными?
а) Фигуру, образованную ломаной линией, конец которой совпадает с её началом (замкнутая ломаная), при условии, что никакие два звена ломаной не имеют общих точек, кроме концов соседних звеньев ломаной, называют многоугольником.
б) Звенья ломаной называют сторонами многоугольника, углы, составленные каждыми двумя соседними сторонами, — углами многоугольника, а эти вершины углов — вершинами многоугольника.
в) Сумму длин сторон многоугольника называют его периметром.
г) Многоугольник называют выпуклым, если он весь расположен по одну сторону от каждой прямой, содержащей его сторону.
д) Два многоугольника называют равными, если их можно совместить при наложении.
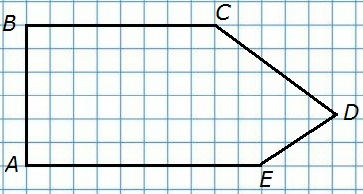
571. Постройте пятиугольник ABCDE. Назовите все его стороны и вершины.
Стороны: AB, BC, CD, DE, EA.
Вершины: A, B, C, D, E.
572. Отрезок, соединяющий две несоседние вершины многоугольника, называют диагональю многоугольника. Например, в четырёхугольнике ABCD отрезка AC и BD — диагонали (рис. 119). Сколько диагоналей в выпуклом:
а) четырёхугольнике;
б) пятиугольнике;
в) шестиугольнике;
г) семиугольнике?

Пусть многоугольник имеет n вершин. Тогда из каждой вершины выходит (n — 3) диагоналей: 1 — сама вершина и 2 — соседние вершины.
Так как диагональ соединяет 2 вершины, значит необходимо (n — 3) разделить пополам и умножить на количество вершин, тогда мы получим, что количество диагоналей n-угольника равняется n • (n — 3) : 2.
а) 4 • (4 — 3) : 2 = 4 • 1 : 2 = 2 (диагонали) — в выпуклом четырёхугольнике;
б) 5 • (5 — 3) : 2 = 5 • 2 : 2 = 10 : 2 = 5 (диагоналей) — в выпуклом пятиугольнике;
в) 6 • (6 — 3) : 2 = 6 • 3 : 2 = 18 : 2 = 9 (диагоналей) — в выпуклом шестиугольнике;
г) 7 • (7 — 3) : 2 = 7 • 4 : 2 = 28 : 2 = 14 (диагоналей) — в выпуклом семиугольнике.
573. Сколько диагоналей в выпуклом: а) десятиугольнике; б) двадцатиугольнике?
а) 10 • (10 — 3) : 2 = 10 • 7 : 2 = 35 (диагоналей) — в выпуклом десятиугольнике;
б) 20 • (20 — 3) : 2 = 20 • 17 : 2 = 170 (диагоналей) — в выпуклом двадцатиугольнике.
Исследуем
574. а) Исследуйте зависимость числа диагоналей (d) выпуклого многоугольника, выходящих из одной его вершины, от числа сторон этого многоугольника (n). Результаты занесите в таблицу.
б) Задайте формулой зависимость d от n.
а) Зависимость: (число диагоналей выпуклого многоугольника, выходящих из одной его вершины, на 3 меньше, чем сторон этого многоугольника)
| n | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
б) d = n — 3.
575. а) Исследуйте зависимость числа диагоналей (d) выпуклого многоугольника от числа его сторон (n). Результаты занесите в таблицу.
б) Задайте формулой зависимость d от n.
а) Зависимость:
| n | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| d | 2 | 5 | 9 | 14 | 20 | 27 | 35 | 44 | 54 |
б) d = n • (n — 3) : 2.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.