Измерение величин
Многоугольники
Ответы к стр. 129
576. Периметры треугольников BCD, BDE и ABE равны соответственно 20 см, 21 см и 22 см, а периметр пятиугольника ABCDE равен 31 см (рис. 120). Определите длины диагоналей BD и BE, если известно, что они равны.
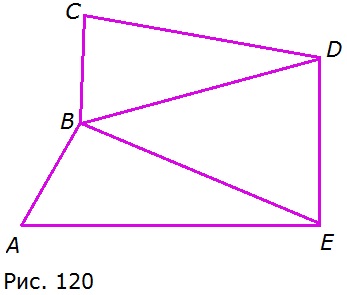
20 + 21 + 22 = 63 (см) — сумма периметров треугольников BCD, BDE и ABE;
Сумма периметров треугольников BCD, BDE и ABE равна периметру пятиугольника ABCDE и удвоенной длине равных отрезков BD и BE, так как:
2BD + 2BE = 4BD (или 4ВЕ), значит:
BD = BE = (63 − 31) : 4 = 8 (см).
О т в е т: BD = BE = 8 см.
577. Считают, что если многоугольники равны, то их площади равны; если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей составляющих его многоугольников. На рисунке 121 изображен прямоугольник ABCD. Верно ли, что площади треугольников ABD и CDB равны? Чему равна площадь треугольника ABD?
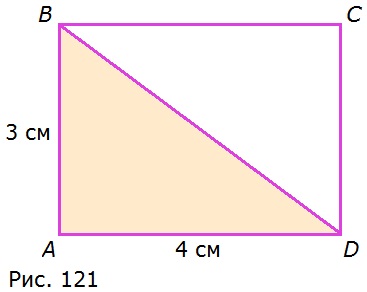
Так как ABCD — прямоугольник, BD — диагональ, то треугольники ABD и BDC совпадают при наложении, то есть равны, а значит, утверждение, что их площади равны верно.
SABCD = 3 • 4 = 12 (см2)
Диагональ делит прямоугольник на 2 равных треугольника, значит, площадь каждого из них равна половине площади прямоугольника ABCD:
SABD = 12 : 2 = 6 (см2)
О т в е т: площадь треугольника ABD равна 6 см2.
Доказываем
578. В прямоугольнике KLMN диагонали KM и LN пересекаются в точке O (рис. 122). Докажите, что площади треугольников KLO и NMO равны.

Так как площадь каждого из треугольников KLN и NMK составляет половину площади одного и того же прямоугольника, то площади этих треугольников равны. Если из этих равных площадей вычесть одну и ту же площадь, а именно — вычесть площадь треугольника KNO, то площади оставшихся треугольников KLO и NMO будут равны.
579. На рисунке 123 показано, как с помощью циркуля и линейки можно построить правильный шестиугольник, у которого стороны равны и углы равны. Постройте в тетради правильный шестиугольник и измерьте его углы.
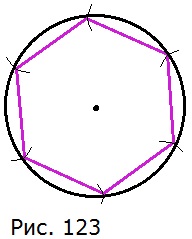
Каждый угол правильного шестиугольника равен 120°.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.