Делимость натуральных чисел
Использование чётности при решении задач
Ответы к стр. 155
703. Записано четыре числа: 0, 0, 0, 1. За один ход разрешается прибавить 1 к любым двум из этих чисел. Можно ли за несколько ходов получить 4 равных числа?
Прибавляя по 1 сразу к двум числам, мы на 2 увеличиваем первоначально нечётную сумму (0 + 0 + 0 + 1 = 1). В результате каждой такой операции получится нечётное число. Значит четыре одинаковых числа (то есть чётную сумму) получить невозможно.
704. В шести коробочках лежат деньги. В первой 1 р., во второй 2 р., в третьей 3 р. и т. д., в шестой 6 р. За один ход разрешается в любые две коробочки добавить по 1 р. Можно ли за несколько ходов уравнять суммы в коробочках?
Всего 3 коробочки (нечётное число) с нечётным числом рублей, значит, сумма рублей в них является нечётным числом. И 3 коробочки (нечётное число) с чётным числом рублей, значит, сумма рублей в них является чётным числом. Если к чётному числу прибавить нечётное, получим нечётное число, поэтому в коробочках лежит нечётное число рублей. Если в любые две коробочки добавить по 1 р., то общая сумма увеличится на 1 • 2 = 2 р., то есть на чётное число. Если к нечётному число прибавить чётное, получим нечётное число, а значит, его невозможно разделить на 6 коробочек (на чётное число). Поэтому уравнять суммы в коробочках нельзя.
705. Не отрывая карандаша от бумаги и не проводя по линии дважды, нарисуйте фигуры, изображённые на рисунке 141.

а) Начинаем рисовать из точки по часовой стрелке прямоугольник, возвращаясь в эту же точку — от неё рисуем линию вниз.
б) Начинаем рисовать из точки по часовой стрелке прямоугольник, возвращаясь в эту же точку — от неё рисуем крышу.
706. Не отрывая карандаша от бумаги и не проводя по линии дважды, попробуйте нарисовать фигуры, изображенные на рисунке 142.
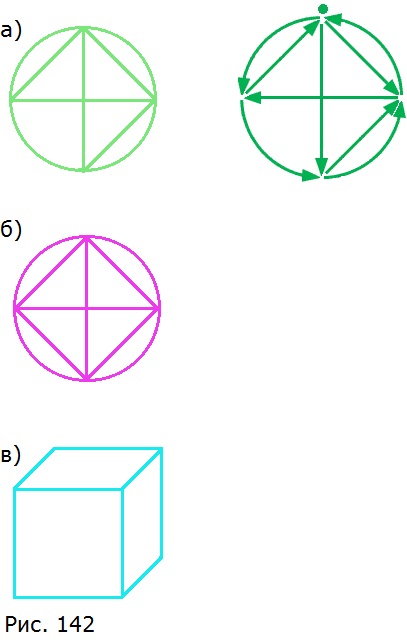
а) Начинаем рисовать из точки линию вниз, затем прорисовываем фигуру внутри круга и далее обводим круг (возвращаемся в соседнюю точку.
б) Невозможно.
в) Невозможно.
707. В задании 706 вам не удалось нарисовать две последние фигуры. Оказывается, этот результат зависит от числа «нечётных» узлов фигуры, в которых сходится нечётное число линий. Сколько «нечётных» узлов должно быть, чтобы фигуру можно было нарисовать?
Чтобы фигуру можно было нарисовать не отрывая карандаша от бумаги и не проводя по линии дважды, «нечётных» узлов должно быть два.
708. Какую из фигур, изображённых на рисунке 143, нельзя нарисовать, не отрывая карандаша от бумаги и не проводя по линии дважды?

а) Два нечетных узла, значит, фигуру нарисовать можно.
б) Все узлы четные, значит, фигуру нарисовать нельзя.
в) Все узлы нечетные, значит, фигуру нарисовать нельзя.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.