Делимость натуральных чисел
Использование чётности при решении задач
Ответы к стр. 156
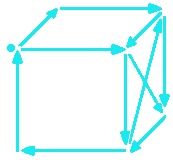
709. Придумайте свои фигуры, которые можно нарисовать, не отрывая карандаша от бумаги и не проводя по линии дважды.
Начинаем рисовать из точки вправо (рисуем квадрат), затем прорисовываем контур верхнего ромба и бокового ромба, далее рисуем пересекающиеся линии через общую сторону ромбов.
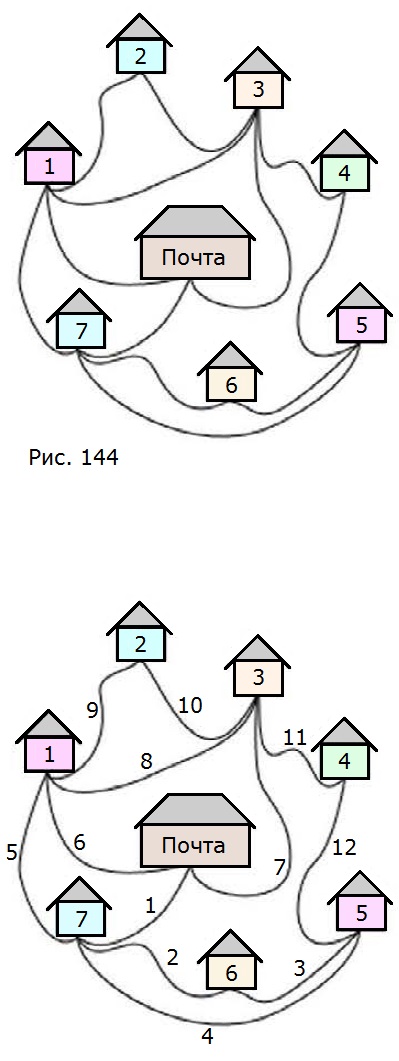
710. Почтальон разнес почту во все дома деревни, после чего зашел с посылкой к Феде. На рисунке 144 показаны все тропинки, по которым проходил почтальон, причем, как оказалось, ни по одной из них он не проходил дважды. В каком доме живет Федя? Каков мог быть маршрут почтальона?
Среди домов есть только два дома, имеющие нечётное число дорог — 5-й дом и Почта. Значит, раз путь был начат от Почты, то последним был дом 5, а следовательно Федя живет в доме номер 5.
711. Экскурсоводу нужно выбрать маршрут по залам музея так, чтобы обойти все залы, не проходя ни через одну дверь дважды. Где нужно начать и где закончить осмотр? Найдите один из возможных маршрутов (рис. 145).
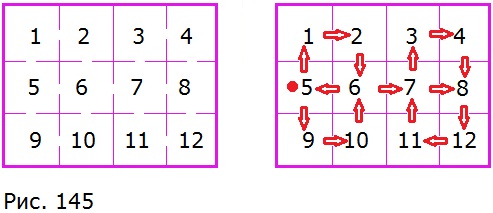
Среди залов музея есть только два, имеющие нечётное число дверей — 5-й и 8-й, значит начать экскурсию можно в одном из них, а закончить в другом. В остальных залах чётное число дверей — они будут пройдены по одному разу, а 6-й и 7-й залы (в которых по 4 двери) — два раза. Возможный маршрут: 5 — 1 — 2 — 6 — 5 — 9 — 10 — 6 — 7 — 3 — 4 — 8 — 12 — 11 — 8.
712. Задача Л. Эйлера. Можно ли поочерёдно обойти все семь мостов г. Кёнигсберга (ныне Калининград), соединяющих районы этого города с островами на реке Прегель (рис. 146), проходя по каждому мосту только один раз?
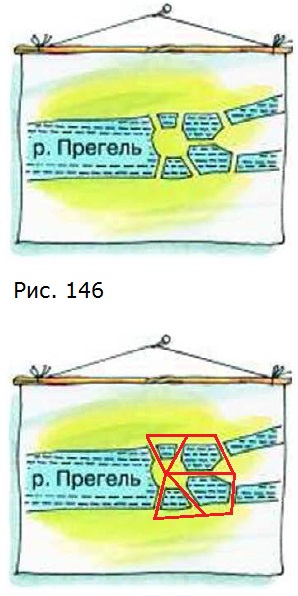
Соединим все проходы по мостам в одну фигуру — получился многоугольник, который имеет четыре «нечётных» угла. Значит невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.