Натуральные числа и нуль
Вычитание
Ответы к стр. 18
61. Найдите неизвестное число, обозначенное буквой х:
а) 43 + x = 64; б) x + 45 = 59;
в) 34 − x = 26; г) x − 53 = 35.
а) 43 + x = 64
х = 64 — 43
х = 21
б) x + 45 = 59
х =59 — 45
х = 14
в) 34 − x = 26
х = 34 — 26
х = 8
г) x − 53 = 35
х = 35 + 53
х= 88
62. Найдите разность чисел 46 и 22. Прибавьте к уменьшаемому и вычитаемому по 1; по 2; по 3 и в каждом случае найдите разность. Сравните полученные результаты.
46 — 22 = 24
(46 + 1) — (22 + 1) = 47 — 23 = 24
(46 + 2) — (22 + 2) = 48 — 24 = 24
(46 + 3) — (22 + 3) = 49 — 25 = 24
Полученные результаты равны.
63. Докажите, что от прибавления к уменьшаемому и вычитаемому одного и того же числа разность не изменяется. То есть, если α − b = c, то (α + n) − (b + n) = c.
(α + n) − (b + n) = α + n − b — n = α — b + n — n = (α — b) + (n — n) = (α — b) + 0 = α — b
Таким образом, (α + n) − (b + n) = α — b.
64. Используя утверждение, сформулированное в предыдущей задаче, вычислите:
а) 68 − 19; б) 35 − 18; в) 65 − 17;
г) 47 − 29; д) 302 − 99; е) 134 − 98;
ж) 200 − 97; з) 132 − 96; и) 649 − 199;
к) 606 − 399; л) 370 − 298; м) 793 − 495.
а) 68 − 19 = (68 + 1) — (19 + 1) = 69 — 20 = 49;
б) 35 − 18 = (35 + 2) — (18 + 2) = 37 — 20 = 17;
в) 65 − 17 = (65 + 3) — (17 + 3) = 68 — 20 = 48;
г) 47 − 29 = (47 + 1) — (29 + 1) = 48 — 30 = 18;
д) 302 − 99 = (302 + 1) — (99 + 1) = 303 — 100 = 203;
е) 134 − 98 = (134 + 2) — (98 + 2) = 136 — 100 = 36;
ж) 200 − 97 = (200 + 3) — (97 + 3) = 203 — 100 = 103;
з) 132 − 96 = (132 + 4) — (96 + 4) = 136 — 100 = 36;
и) 649 − 199 = (649 + 1) — (199 + 1) = 650 — 200 = 450;
к) 606 − 399 = (606 + 1) — (399 + 1) = 607 — 400 = 207;
л) 370 − 298 = (370 + 2) — (298 + 2) = 372 — 300 = 72;
м) 793 − 495 = (793 + 5) — (495 + 5) = 798 — 500 = 298.
65. Выполните действия «цепочкой» по образцу:
75 − 5 + 17 − 20 = 70 + 17 − 20 = 87 − 20 = 67.
а) 18 + 9 − 23 + 32; б) 33 − 6 + 25 − 17;
в) 37 − 33 + 19 − 3; г) 53 + 12 − 15 + 17;
д) 14 − 6 + 29 − 11; е) 45 + 25 − 18 + 101;
ж) 38 + 3 − 5 − 28; з) 64 − 16 + 19 − 2.
а) 18 + 9 − 23 + 32 = 27 — 23 + 32 = 4 + 32 = 36;
б) 33 − 6 + 25 − 17 = 27 + 25 — 17 = 52 — 17 = 35;
в) 37 − 33 + 19 − 3 = 4 + 19 — 3 = 23 — 3 = 20;
г) 53 + 12 − 15 + 17 = 65 — 15 + 17 = 50 + 17 = 67;
д) 14 − 6 + 29 − 11 = 8 + 29 — 11 = 37 — 11 = 26;
е) 45 + 25 − 18 + 101 = 70 — 18 + 101 = 52 + 101 = 153;
ж) 38 + 3 − 5 − 28 = 41 — 5 — 28 = 36 — 28 = 8;
з) 64 − 16 + 19 − 2 = 48 + 19 — 2 = 67 — 2 = 65.
66. а) Задумали число, увеличили его на 45 и получили 66 (рис.1, а). Каким действием можно найти задуманное число? Найдите его.
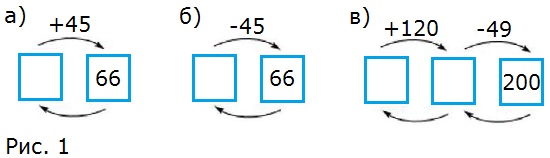
б) Задумали число, уменьшили его на 45 и получили 66 (рис.1, б). Найдите задуманное число.
в) Задумали число, увеличили его на 120, результат уменьшили на 49. Получили 200 (рис.1, в). Найдите задуманное число.
а) 66 — 45 = 21;
б) 66 + 45 = 111;
в) 200 + 49 — 120 = 129.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.