Измерение величин
Измерение отрезков
Ответы к стр. 83
367. Точка С расположена на прямой между точками A и B. Длина отрезка AC равна 8 см, длина отрезка CB на 3 см больше длины отрезка AC. Найдите длину отрезка AB.
1) 8 + 3 = 11 (см) — длина отрезка СВ
2) 8 + 11 = 19 (см) — длина отрезка АВ
О т в е т: отрезок АВ 19 см.
368. Точка A расположена на прямой между точками B и C. Длина отрезка CB на 3 см больше длины отрезка AC. Найдите длину отрезка AB.
Точка А делит отрезок ВС на отрезок ВА и отрезок АС. Тогда длина отрезка АВ = ВС — АС. Но длина отрезка СВ = АС + 3 (см). Подставляем в первое выражение длину отрезка СВ из второго выражение: АВ = ВС — АС = (АС + 3) — АС = АС + 3 — АС = 3 (см).
О т в е т: отрезок АВ 3 см.
369. На прямой даны точки A, B и C, причем AB = 6 см, AC = 13 см. Найдите длину отрезка BC, если:
а) точки B и C лежат по одну сторону от точки A;
б) точки B и C лежат по разные стороны от точки A.
а) Получается отрезок АС, разделённый точкой В на отрезки АВ и ВС. Тогда длина отрезка ВС = АС — АВ = 13 — 6 = 7 (см).
О т в е т: отрезок ВС 7 см.
б) Получается отрезок ВС, разделённый точкой А на отрезки ВА и АС. Тогда длина отрезка ВС = ВА + АС = 6 + 13 = 19 (см).
О т в е т: отрезок ВС 19 см.
370. На прямой даны три точки A, B и C, причем AB = 13 см, AC = 4 см. Найдите длину отрезка BC. (Задача имеет два решения.)
Так как АВ > АС, то возможно 2 решения: точка В не может делить отрезок АС на отрезки АВ и ВС, поскольку отрезок АВ будет больше исходного отрезка АС.
1) Точка С делит отрезок АВ на отрезки АС и СВ. Тогда длина отрезка ВС = АВ — АС = 13 — 4 = 9 (см).
О т в е т: отрезок ВС 9 см.
2) Точка А делит отрезок СВ на отрезки СА и АВ. Тогда длина отрезка ВС = СА + АВ = 4 + 13 = 17 (см).
О т в е т: отрезок ВС 17 см.
371. На прямой даны три точки A, B и C, причем AB = 83 см, AC = 97 см. Найдите длину отрезка BC. Сколько решений имеет задача?
Так как АС > АВ, то возможно 2 решения: точка С не может делить отрезок АВ на отрезки АС и СВ, поскольку отрезок АС будет больше исходного отрезка АВ.
1) Точка В делит отрезок АС на отрезки АВ и ВС. Тогда длина отрезка ВС = АС — АВ = 97 — 83 = 14 (см).
О т в е т: отрезок ВС 14 см.
2) Точка А делит отрезок ВС на отрезки ВА и АС. Тогда длина отрезка ВС = ВА + АС = 83 + 97 = 180 (см).
О т в е т: отрезок ВС 180 см.
372. На луче AM отложили отрезки AB и AC, AC = 89 см. Найдите длину отрезка BC, если:
а) AB на 15 см длиннее AC;
б) AB на 15 см короче AC.
а) В этом случае точка С лежит между точками А и В и делит отрезок АВ на отрезки АС и СВ, поскольку исходный отрезок АВ не может быть меньше отрезка АС. Тогда:
1) АВ = АС + 15 = 89 + 15 = 104 (см)
2) ВС = АВ — АС = 104 — 89 = 15 (см)
О т в е т: отрезок ВС 15 см.
б) В этом случае точка В лежит между точками А и С и делит отрезок АС на отрезки АВ и ВС, поскольку исходный отрезок АС не может быть меньше отрезка АВ. Тогда:
1) АВ = АС — 15 = 89 — 15 = 74 (см)
2) ВС = АС — АВ = 89 — 74 = 15 (см)
О т в е т: отрезок ВС 15 см.
373. Объясните на примере, как измерить длину отрезка с точностью до 1 см.
а) с недостатком; б) с избытком; в) с округлением.
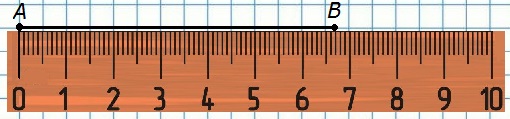
Если приложить шкалу сантиметровой линейки к отрезку АВ так, что отметка «0» совпадёт с точкой А, то окажется, что точка В не совпадает с делением шкалы на отметке «6» или «7». При этом величины 6 см и 7 см отличаются от АВ не более чем на 1 см и называются приближёнными значениями длины АВ с точностью до 1 см.
а) длина отрезка АВ равна 6 см с недостатком с точностью до 1 см;
б) длина отрезка АВ равна 7 см с избытком с точностью до 1 см;
в) длина отрезка АВ равна 7 см с округлением с точностью до 1 см, поскольку точка В находится ближе к отметке «7», а не «6».
374. Измерьте длину и ширину тетради с точностью до 1 см:
а) с недостатком; б) с избытком; в) с округлением.
а) длина 20 см, ширина 16 см;
б) длина 21 см, ширина 17 см;
в) длина 21 см, ширина 17 см.
375. Отметьте в тетради две точки. Определите на глаз расстояние между ними. Начертите отрезок с концами в этих точках и измерьте приближенно его длину.
376. С помощью линейки измерьте отрезки, изображенные на рисунке 53, с точностью до 1 см:
а) с недостатком; б) с избытком; в) с округлением.
АВ = 2 см 5 мм, СD = 3 см 3 мм, EF = 2 см 8 мм
а) АВ ≈ 2 см, СD ≈ 3 см, EF ≈ 2 см;
б) АВ ≈ 3 см, СD ≈ 4 см, EF ≈ 3 см;
в) АВ ≈ 3 см, СD ≈ 3 см, EF ≈ 3 см.
377. Рейка длиной 147 см разрезана на 4 равные части. Какую длину имеет каждая часть с точностью до 1 см:
а) с недостатком; б) с избытком; в) с округлением?
147 : 4 = 36 (ост. 3)
а) 36 см;
а) 37 см;
б) 37 см.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
