Натуральные числа
Натуральные числа и шкалы
Плоскость. Прямая. Луч
Ответы к стр. 18
79. Отметьте точки А и В на расстоянии 2 см друг от друга. Проведите через эти точки прямую и отложите на ней отрезок АС длиной в 5 см так, чтобы точки В и С были по разные стороны от точки А. Есть ли на прямой точка, находящаяся от точки А на расстоянии 1 см?

Такой точки нет.
80. На сколько частей делят плоскость две пересекающиеся прямые?
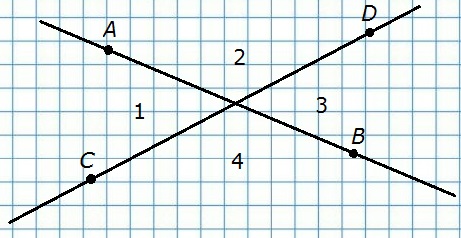
На четыре части.
81. Начертите треугольник ABC. На сколько частей делят плоскость прямые АВ, АС и ВС?
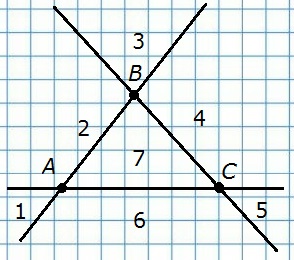
На семь частей.
82. По рисунку 16 назовите: 3 точки, 2 отрезка, прямую и 4 луча.
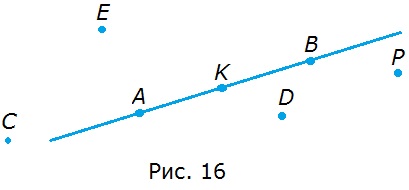
Точки C, E, D. Отрезки АК, КВ. Прямая АВ. Лучи AK, AB, BK, BA.
83. Начертите луч АХ и отложите на нём от его начала один за другим 3 отрезка по 2 см каждый. Можно ли на этом луче отложить 1000 таких отрезков?

На луче AX можно отложить любое натуральное число отрезков, в том числе и 1000.
84. Вычислите устно:
а) 35 + 5; б) 43 — 6; в) 6 • 7; г) 64 • 10; д) 72 : 9;
59 + 1; 30 — 1; 9 • 4; 50 : 10; 48 : 6;
87 + 3; 51 — 4; 8 • 8; 70 • 10; 56 : 7;
44 + 6; 27 — 8; 5 • 9; 100 : 100; 81 : 9;
28 + 12; 24 — 7; 9 • 6; 100 • 100; 40 : 8.
а) 35 + 5 = 40; б) 43 — 6 = 37; в) 6 • 7 = 42;
59 + 1 = 60; 30 — 1 = 29; 9 • 4 = 36;
87 + 3 = 90; 51 — 4 = 47; 8 • 8 = 64;
44 + 6 = 50; 27 — 8 = 19; 5 • 9 = 45;
28 + 12 = 40; 24 — 7 = 17; 9 • 6 = 54;
г) 64 • 10 = 640; д) 72 : 9 = 8;
50 : 10 = 5; 48 : 6 = 8;
70 • 10 = 700; 56 : 7 = 8;
100 : 100 = 1; 81 : 9 = 9;
100 • 100 = 10000; 40 : 8 = 5.
85. Заполните таблицу:
| Уменьшаемое | 37 | 55 | 49 | 38 | 18 | 54 | 68 | 51 |
| Вычитаемое | 17 | 20 | 10 | 19 | 1 | 16 | 23 | 29 |
| Разность | 20 | 35 | 39 | 19 | 17 | 38 | 45 | 22 |
86. Вычислите устно и объясните приём вычислений:
а) 270 : 9; б) 1224 : 12; в) 300 • 6; г) 801 • 7.
а) 270 : 9 = (27 • 10) : 9 = (27 : 9) • 10 = 3 • 10 = 30;
б) 1224 : 12 = (1200 + 24) : 12 = 1200 : 12 + 24 : 12 = 100 + 2 = 102;
в) 300 • 6 = 3 • 100 • 6 = 3 • 6 • 100 = 18 • 100 = 1800;
г) 801 • 7 = (800 + 1) • 7 = 800 • 7 + 1 • 7 = 8 • 100 • 7 + 7 = 8 • 7 • 100 + 7 = 56 • 100 + 7 = 5600 + 7 = 5607.
87. Может ли сумма двух чисел равняться разности этих же чисел?
Может, если одно из этих чисел 0: 48 + 0 = 48, 48 — 0 = 48.
88. Не выполняя вычислений, определите, сколько цифр будет в частном:
а) 825 : 5; б) 2952 : 24; в) 11 174 : 37; г) 724 200 : 75.
а) 825 : 5 → 825, первое неполное частное 8, следовательно, в частном будет три цифры;
б) 2952 : 24 → 2952, первое неполное частное 29, следовательно, в частном будет три цифры;
в) 11 174 : 37 → 11 174, первое неполное частное 111, следовательно, в частном будет три цифры;
г) 724 200 : 75 → 724 200, первое неполное частное 724, следовательно, в частном будет четыре цифры.
89. Сложите:
а) 3 м 45 см и 1 м 20 см; в) 2 м 80 см и 4 м 60 см;
б) 7 дм 8 см и 19 см; г) 1 км 250 м и 800 м.
а) 3 м 45 см + 1 м 20 см = (3 м + 1 м) + (45 см + 20 см) = 4 м + 65 см = 4 м 65 см;
б) 7 дм 8 см и 19 см = 78 см + 19 см = 97 см = 9 дм 7 см;
в) 2 м 80 см и 4 м 60 см = (2 м + 4 м) + (80 см + 60 см) = 6 м + 1 м 40 см = (6 м + 1 м) + 40 см = 7 м + 40 см = 7 м 40 см;
г) 1 км 250 м и 800 м = 1 км + (250 м + 800 м) = 1 км + 1 км 50 м = (1 км + 1 км) + 50 м = 2 км + 50 м = 2 км 50 м.
90. Начертите отрезки MP, РК, КС такие, что: MP = 3 см, РК = 2 см 5 мм и КС = 4 см 8 мм.
![]()
91. Начертите пятиугольник ABCDE. Отметьте точку М на стороне АВ и точку N на стороне CD. Соедините точки М и N отрезком. Какие получились многоугольники? Назовите их.
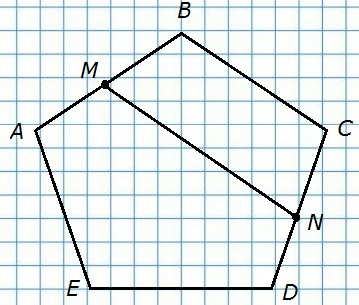
Пятиугольник AMNDE и четырёхугольник MBCN.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И