Рациональные числа
Изображение рациональных чисел на координатной оси
Ответы к стр. 119
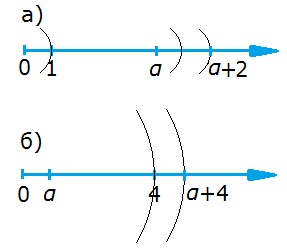
609. На координатном луче отмечены числа. С помощью циркуля отметьте на координатном луче число:
а) α + 2 (рис. 61, а); б) α + 4 (рис. 61, б).

а) Нужно циркулем измерить расстояние от нуля до единицы, затем от точки α отложить это расстояние вправо два раза.
б) Нужно циркулем измерить расстояние от нуля до четырёх, затем от точки α отложить это расстояние вправо.
610. Для чисел α и b выполняется равенство 5 — α = b. С помощью циркуля отметьте на координатном луче число α + b (рис. 62).

5 — α = b, тогда α + b = 5
Нужно циркулем измерить расстояние от нуля до единицы, затем от единицы отложить это расстояние вправо четыре раза.

611. Для чисел α и b выполняется равенство α — 3 = b. С помощью циркуля отметьте на координатном луче число α (рис. 63).
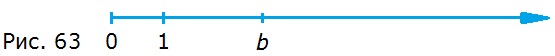
α — 3 = b, тогда α = b + 3
Нужно циркулем измерить расстояние от нуля до единицы, затем от точки b отложить это расстояние вправо три раза.

612. На координатной оси отмечены точки с координатами: 0, 1, b (рис. 64). С помощью циркуля постройте точки с координатами: -1, —b, b + 1, b — 1, 1 — b, —b — 1.
![]()
Точка с координатой -1: нужно циркулем измерить расстояние от нуля до единицы, затем от нуля отложить это расстояние влево.
Точка с координатой —b: нужно циркулем измерить расстояние от нуля до точки b, затем от нуля отложить это расстояние влево.
Точка с координатой b + 1: нужно циркулем измерить расстояние от нуля до единицы, затем от точки b отложить это расстояние вправо.
Точка с координатой b — 1: нужно циркулем измерить расстояние от нуля до единицы, затем от точки b отложить это расстояние влево.
Точка с координатой 1 — b: нужно циркулем измерить расстояние от нуля до точки b, затем от единицы отложить это расстояние влево.
Точка с координатой —b — 1: нужно циркулем измерить расстояние от нуля до единицы, затем от точки —b отложить это расстояние влево.

613. На координатной оси отмечены точки с координатами: 0, α, b. С помощью циркуля постройте точки с координатами: —α, —b, α + b, α — b, b — α, —α — b (рис. 65).
![]()
Точка с координатой —α: нужно циркулем измерить расстояние от нуля до точки α, затем от нуля отложить это расстояние влево.
Точка с координатой —b: нужно циркулем измерить расстояние от нуля до точки b, затем от нуля отложить это расстояние влево.
Точка с координатой α + b: нужно циркулем измерить расстояние от нуля до точки b, затем от точки α отложить это расстояние вправо.
Точка с координатой α — b: нужно циркулем измерить расстояние от нуля до точки b, затем от точки α отложить это расстояние влево.
Точка с координатой b — α: нужно циркулем измерить расстояние от нуля до точки α, затем от точки b отложить это расстояние влево.
Точка с координатой —α — b: нужно циркулем измерить расстояние от нуля до точки b, затем от точки —α отложить это расстояние влево.

614. На рисунке 66 указаны координаты точек А и В. Найдите координату точки С.
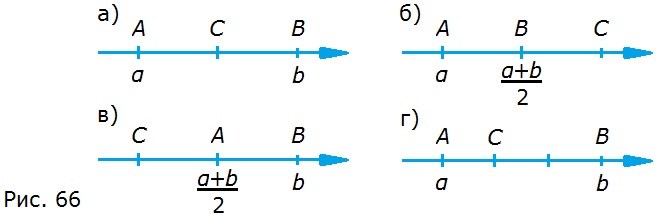
а) Точка С — середина отрезка АВ, тогда координата т. С = (А + В) : 2 = α+b/2.
б) Точка В — середина отрезка АС, тогда координата т. В = (А + С) : 2, а координата т. С = 2В — А = 2 • α+b/2 — α = 2(α+b)/2 — α = α + b — α = b.
в) Точка А — середина отрезка СВ, тогда координата т. А = (С + В) : 2, а координата т. С = 2А — В = 2 • α+b/2 — b = 2(α+b)/2 — b = α + b — b = α.
г) Длина отрезка АВ = b — α, этот отрезок разделён на три равные части, тогда длина одной части b—α/3. Координата точки С — это сумма координаты точки А и длины одной части — отрезка АС: α + b—α/3 = 3α/3 + b—α/3 = 3α+b—α/3 = 2α+b/3.
| ← Предыдущая | Следующая → |
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.