Отношения, пропорции, проценты
Вероятность события
Ответы к стр. 39
162. Бросают игральный кубик. Подсчитайте вероятность события:
а) А: «выпадет 5 очков»;
б) B: «выпадает четное число очков»;
в) С: «выпадает нечетное число очков»;
г) D: «выпадает число очков, кратное 3».
Вероятностью события А называют отношение количества случаев, благоприятствующих событию А, к числу всех равновозможных случаев, один из которых обязательно произойдет.
а) Всего на кубике 6 граней, то есть число всех равновозможных случаев равно 6. 5 очков находится только на одной грани, то есть количество случаев, благоприятствующих событию, равно 1. Тогда вероятность события А (выпадение 5 очков) равна 1/6.
б) Всего на кубике 6 граней, то есть число всех равновозможных случаев равно 6. На трёх гранях расположены чётные очки: 2, 4, 6, поэтому количество случаев, благоприятствующих событию, равно 3. Тогда вероятность события В (выпадение чётного числа очков) равна 3/6 = 1/2.
в) Всего на кубике 6 граней, то есть число всех равновозможных случаев равно 6. На трёх гранях расположены нечётные очки: 1, 3, 5, поэтому количество случаев, благоприятствующих событию, равно 3. Тогда вероятность события С (выпадение нечётного числа очков) равна 3/6 = 1/2.
г) Всего на кубике 6 граней, то есть число всех равновозможных случаев равно 6. На двух гранях расположены очки кратные трём: 3, 6, поэтому количество случаев, благоприятствующих событию, равно 2. Тогда вероятность события D (выпадение числа очков, кратного 3), равна 2/6 = 1/3.
163. Задачи Даламбера. а) Монета бросается два раза. Какова вероятность того, что хотя бы один раз выпадет герб?
б) Монета бросается три раза. Какова вероятность того, что герб выпадет по крайней мере один раз?
а) В результате двух последовательных подбрасываний монеты возможно 4 исхода:
1) герб, герб;
2) герб, цифра;
3) цифра, герб;
4) цифра, цифра.
Из них в трёх случаях (1, 2 и 3) выпадает герб. Следовательно, вероятность выпадения герба равна 3/4.
б) В результате трёх последовательных подбрасываний монеты возможно 8 исходов:
1) герб, герб, герб;
2) герб, герб, цифра;
3) герб, цифра, герб;
4) герб, цифра, цифра;
5) цифра, герб, герб;
6) цифра, герб, цифра;
7) цифра, цифра, герб;
8) цифра, цифра, цифра.
Из них в семи случаях (1, 2, 3, 4, 5, 6, 7) выпадает герб. Следовательно, вероятность выпадения герба равна 7/8.
164. Из ящика, где находятся 2 чёрных и 5 белых шаров, вынут наугад один шар. Какова вероятность того, что вынут:
а) чёрный шар; б) белый шар.
Число всех равновозможных случаев равно 7, так как в ящике всего 7 шаров.
а) Количество случаев, благоприятствующих выпадению чёрного шара равно 2, так как в ящике 2 чёрных шара. Вероятность выпадения чёрного шара равна 2/7.
б) Количество случаев, благоприятствующих выпадению белого шара равно 5, так как в ящике 5 белых шаров. Вероятность выпадения белого шара равна 5/7.
165. Подбросьте монету 50 раз. Сколько раз выпал орёл?
Вероятность выпадения орла 1/2, то есть он должен выпасть 25 раз.
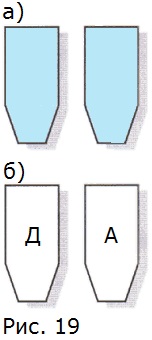
166. На двух карточках написали буквы А и Д, положили карточки на стол буквами вниз в произвольном порядке (рис. 19, а). Какова вероятность того, что после переворачивания карточек получится слово «ДА» (рис. 19, б)?
Так как карточки могут сформировать либо слово «АД», либо слово «ДА», то число всех равновозможных случаев, одно из которых обязательно произойдёт при переворачивании карточек равно 2.
Количество случаев, благоприятствующих формированию слова «ДА» равно 1, тогда вероятность формирования слова «ДА» равна 1/2.
167. На трёх карточках написали буквы Е, Н, Т, положили карточки на стол буквами вниз в произвольном порядке. Какова вероятность того, что после переворачивания карточек получится слово «НЕТ».
При переворачивании первой карточки на ней может оказаться одна из трёх букв. На второй карточке может оказаться одна из двух оставшихся букв, а на третьей — последняя оставшаяся буква. Тогда общее количество полученных сочетаний букв будет 3 • 2 • 1 = 6 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при переворачивании карточек, равно 6.
Количество случаев, благоприятствующих формированию слова «НЕТ» равно 1, тогда вероятность формирования слова «НЕТ» равна 1/6.
168. На четырёх карточках написали буквы К, О, Л, Я, положили карточки на стол буквами вниз в произвольном порядке. Какова вероятность того, что после переворачивания карточек получится имя КОЛЯ?
При переворачивании первой карточки на ней может оказаться одна из четырёх букв. На второй карточке может оказаться одна из трёх оставшихся букв, на третьей — одна из двух оставшихся букв и на четвёртой — последняя оставшаяся буква. Тогда общее количество полученных сочетаний букв будет 4 • 3 • 2 • 1 = 24 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при переворачивании карточек, равно 24.
Количество случаев, благоприятствующих формированию слова «КОЛЯ» равно 1, тогда вероятность формирования слова «КОЛЯ» равна 1/24.
169. На четырёх карточках написали буквы А, С, А, Ш, положили карточки на стол буквами вниз в произвольном порядке. Какова вероятность того, что после переворачивания карточек получится имя САША?
При переворачивании первой карточки на ней может оказаться одна из четырёх букв. На второй карточке может оказаться одна из трёх оставшихся букв, на третьей — одна из двух оставшихся букв и на четвёртой — последняя оставшаяся буква. Тогда общее количество полученных сочетаний букв будет 4 • 3 • 2 • 1 = 24 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при переворачивании карточек, равно 24.
Количество случаев, благоприятствующих формированию слова «САША» равно 2, так как буква «А» встречается 2 раза. Тогда вероятность формирования слова «САША» равна 2/24 = 1/12
170. Синоптики обещают на следующей неделе 2 солнечных дня и 5 пасмурных. Какое событие более вероятно: «воскресенье − солнечный день» или «воскресенье − пасмурный день»?
Число всех равновозможных случаев, одно из которых обязательно произойдет на неделе равно 2 + 5 = 7 дней.
Количество случаев, благоприятствующих условию «воскресенье — солнечный день» равно 2, так как солнечный день может быть 2 раза в неделю. Количество случаев, благоприятствующих условию «воскресенье — пасмурный день» равно 5, так как пасмурный день может быть 5 раз в неделю.
Вероятность события «воскресенье — солнечный день» = 2/7.
Вероятность события «воскресенье — пасмурный день» = 5/7.
5/7 > 2/7, следовательно, выше вероятность события «воскресенье — пасмурный день».
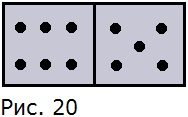
171. Из 28 костей домино выбирают наугад одну кость (на рисунке 20 изображена кость с суммой очков 11). Какова вероятность выбрать кость с суммой очков:
а) 0; б) 2; в) 6; г) 10.
Число всех равновозможных случаев, одно из которых обязательно произойдет при выборе кости домино равно 28, так как всего костей домино 28.
а) Количество случаев, благоприятствующих выбору кости с 0 очков равна 1, так как только 1 кость имеет такое количество очков, поэтому вероятность равна 1/28.
б) Количество случаев, благоприятствующих выбору кости с 2 очками равна 2, так как 2 кости имеют такое количество очков: 0 + 2 и 1 + 1, поэтому вероятность равна 2/28 = 1/14.
в) Количество случаев, благоприятствующих выбору кости с 6 очками равна 4, так как 4 кости имеют такое количество очков: 0 + 6, 1 + 5, 2 + 4, 3 + 3, поэтому вероятность равна 4/28 = 1/7.
г) Количество случаев, благоприятствующих выбору кости с 10 очками равна 2, так как 2 кости имеют такое количество очков: 4 + 6, 5 + 5, поэтому вероятность равна 2/28 = 1/14.
| ← Предыдущая | Следующая → |
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.