Целые числа
Фигуры на плоскости, симметричные относительно точки
Ответы к стр. 81
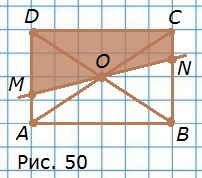
400. По рисунку 50 определите, какой фигуре симметричен относительно точки O:
а) треугольник BCO; б) треугольник ADC;
в) треугольник CNO; г) прямоугольник ABCD;
д) четырехугольник DCNM.
Две фигуры называются симметричными если каждой точке одной фигуры соответствует симметричная точка другой фигуры.
а) точкам B, C, O относительно точки O симметричны точки D, A, O, следовательно, треугольник BCO относительно точки O симметричен треугольнику DAO;
б) точкам A, D, C относительно точки O симметричны точки C, B, A, следовательно, треугольник ADC относительно точки O симметричен треугольнику CBA;
в) точкам C, N, O относительно точки O симметричны точки A, M, O, следовательно, треугольник CNO относительно точки O симметричен треугольнику AMO;
г) точкам A, B, C, D относительно точки O симметричны точки C, D, A, B, следовательно, прямоугольник ABCD относительно точки O симметричен прямоугольнику CDAB;
д) точкам D, C, N, M относительно точки O симметричны точки B, A, M, N, следовательно, четырёхугольник DCNM относительно точки O симметричен четырехугольнику BAMN.
401. На клетчатой бумаге изображен прямоугольник 3×4 (рис. 51). Найдите пять способов разрезания прямоугольника на две равные части так, чтобы линия разреза шла по линиям клетчатой бумаги.
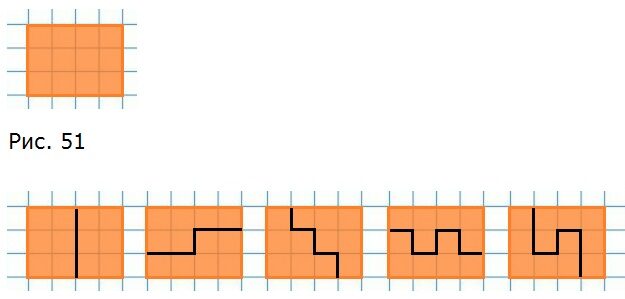
402. На клетчатой бумаге изобразите прямоугольник 3×5, из которого удален центральный квадрат (рис. 52). Найдите пять способов разрезания оставшейся фигуры на две равные части так, чтобы линия разреза шла по линиям клетчатой бумаги.
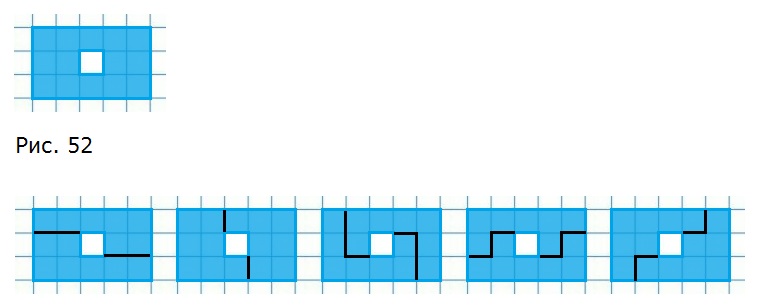
403. На клетчатой бумаге изображён квадрат 6×6. Найдите шесть способов разрезания квадрата на две равные части так, чтобы линия разреза шла по линиям клетчатой бумаги.
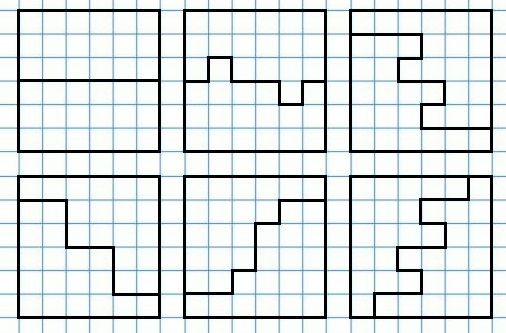
404. Можно ли квадрат 5×5, изображённый на клетчатой бумаге, разрезать на две равные части так, чтобы линия разреза шла по линиям клетчатой бумаги?
Площадь такого квадрата 5 × 5 = 25 клеток. Если квадрат разделить пополам, то в каждой половине будет 25 : 2 = 12 1/2, то есть какую-то клетку придется делить не по линии клетчатой бумаги, значит разделить так квадрат нельзя.
Доказываем
405. Докажите, что любая прямая, проходящая через центр симметрии прямоугольника, делит его на две равные части.
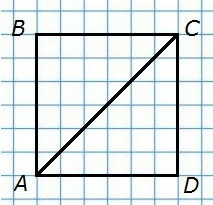
Возьмем прямоугольник ABCD и проведем через его центр симметрии прямую АС. Раз прямая проведена через центр симметрии то получается, что точка A симметрична сама себе и точка С симметрична сама себе, а точка B симметрична точке D, следовательно, треугольник АВС равен треугольнику АDС. Кроме того, если треугольник АDС повернуть на 180о, то он совместится с треугольником АВС. Как бы не была проведена прямая через центр симметрии прямоугольника, она делит прямоугольник на две фигуры, причём точки одной фигуры всегда симметричны точкам другой фигуры.
406. Докажите, что любая прямая, проходящая через центр симметрии фигуры, делит её на две равные части.
Если через центр симметрии фигуры провести прямую, то эта прямая разделит фигуру на две половины. Между симметричными точками и центром симметрии можно построить два равных отрезка, например, AO = OB, где точка О — центр симметрии. Такие же равные отрезки можно построить, используя любую из множества симметричных точек, из которых состоят обе половины фигуры. Следовательно, если одну половину фигуры развернуть на 180о относительно прямой, проходящей через центр симметрии, то первая половина совместится со второй половиной фигуры, а это значит что две половины равны.
407. Постройте окружность с центром О. Отметьте на ней точку М. Постройте точку N, симметричную точке М относительно точки О. Верно ли, что окружность симметрична относительно своего центра?
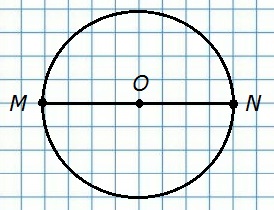
Точка М симметрична точке N относительно точки О, следовательно, MO = ON. Такие же равные отрезки можно построить, используя все множество симметричных точек, из которых состоит окружность, и если одну половину окружности развернуть на 180о относительно прямой МN, проходящей через центр симметрии, то первая половина совместится со второй половиной окружности, а это значит, что две половины равны. Получается, что окружность симметрична относительно своего центра.
408. Постройте круг с центром О. Отметьте внутри круга точку М. Постройте точку N, симметричную точке М относительно точки О. Верно ли, что круг симметричен относительно своего центра?
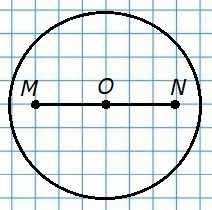
Точка М симметрична точке N относительно точки О, следовательно, MO = ON. Такие же равные отрезки можно построить, используя все множество симметричных точек, из которых состоит круг. Так как для любой точки круга симметричная ей точка тоже будет принадлежать кругу, то круг будет симметричен относительно своего центра.
| ← Предыдущая | Следующая → |
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.