Целые числа
Фигуры на плоскости, симметричные относительно точки
Ответы к стр. 82
409. Дан отрезок AB и точка O вне этого отрезка. Постройте отрезок A1B1, симметричный отрезку AB, так, чтобы точки A и A1, B и B1, были симметричны относительно точки О. Соедините точки A и B1, A1 и B. Укажите все пары отрезков, симметричных друг другу относительно точки О. Какие из построенных отрезков симметричны сами себе относительно точки О?
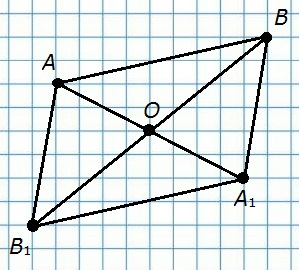
Пары отрезков, симметричные друг другу относительно точки O:
AB и A1B1;
AB1 и A1B;
AO и A1O;
BO и B1O.
Отрезки симметричные сами себе относительно точки O:
AA1;
B1B.
410. Дан треугольник ABC. Постройте треугольник, симметричный треугольнику ABC относительно точки A.
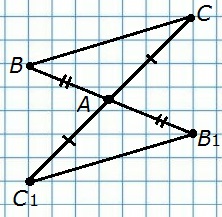
411. Постройте треугольник, симметричный треугольнику ABC относительно точки O, лежащей на стороне AB.
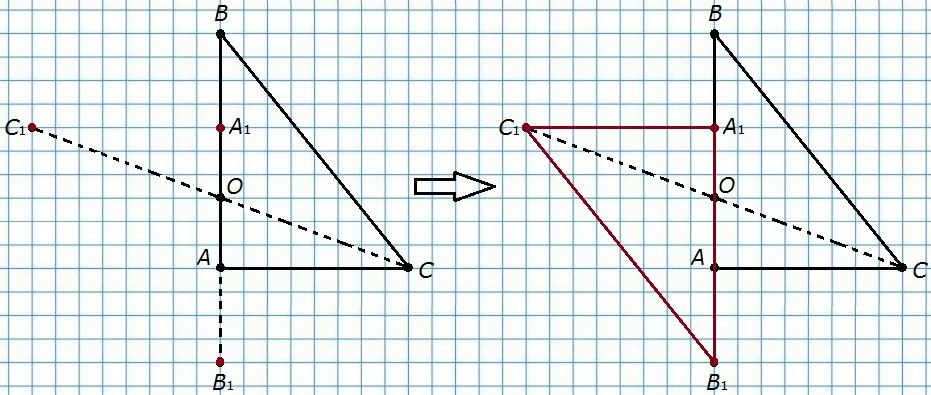
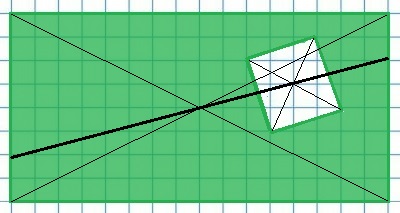
412. Из прямоугольника вырезали квадрат (рис. 53). Постройте прямую, которая делит площадь закрашенной фигуры пополам.
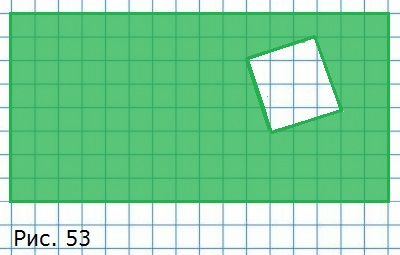
Прямая, проходящая через центр симметрии фигуры, делит эту фигуру пополам. Центром симметрии прямоугольника будет точка пересечения его диагоналей. Центром симметрии квадрата также будет точка пересечения его диагоналей. Проведём через центры симметрий прямоугольника и квадрата прямую — она и будет делить площадь закрашенной фигуры пополам.
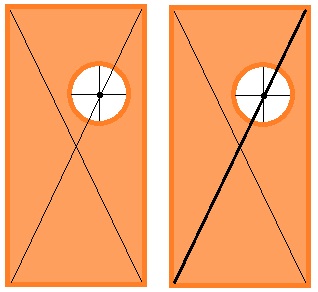
413. Вороне как-то Бог послал кусочек сыра… Предположим, что, в отличие от героини известной басни, наша Ворона захотела разделить сыр поровну с Лисицей. Как она должна разрезать по прямой кусок сыра, если этот кусок имеет форму прямоугольника с круглой дыркой (рис. 54)? (Толщина куска сыра во всех местах одна и та же.)

Прямая, проходящая через центр симметрии фигуры, делит эту фигуру пополам. Центром симметрии прямоугольника будет точка пересечения его диагоналей. Центром симметрии круга будет точка пересечения его диаметров или центр круга. Проведём через центры симметрий прямоугольника и круга прямую — она и будет делить площадь закрашенной фигуры пополам. Эта прямая совпадает с одной из диагоналей прямоугольника.
| ← Предыдущая | Следующая → |
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.