Алгебраические выражения
Формулы сокращённого умножения
Квадрат суммы
Ответы к стр. 101
340. Используя формулу квадрата суммы, преобразуйте выражение в многочлен стандартного вида:
а) (α2 + b)2; б) (x + y3)2; в) (m2 + n2)2;
г) (p3 + q5)2; д) (αb + c)2; е) (x + yz)2;
ж) (3m + n3)2; з) (2p + 3q2)2; и) (3αb2 + 2c3)2.
а) (α2 + b)2 = (α2)2 + 2α2b + b2 = α4 + 2α2b + b2;
б) (x + y3)2 = x2 + 2xy3 + (y3)2 = x2 + 2xy3 + y6;
в) (m2 + n2)2 = (m2)2 + 2m2n2 + (n2)2 = m4 + 2m2n2 + n4;
г) (p3 + q5)2 = (p3)2 + 2p3q5 + (q5)2 = p6 + 2p3q5 + q10;
д) (αb + c)2 = (αb)2 + 2αbc + c = α2b2 + 2αbc + c2;
е) (x + yz)2 = x2 + 2xyz + (yz)2 = x2 + 2xyz + y2z2;
ж) (3m + n3)2 = (3m)2 + 2•3m•n3 + (n3)2 = 9m2 + 6mn3 + n6;
з) (2p + 3q2)2 = (2p)2 + 2•2p•3q2 + (3q2)2 = 4p2 + 12pq2 + 9q4;
и) (3αb2 + 2c3)2 = (3αb2)2 + 2•3αb2•2c3 + (2c3)2 = 9α2b4 + 12αb2c3 + 4c6.
341. Преобразуйте выражение в многочлен:
а) (1/2 + α)2; б) (x + 1/3)2; в) (m + 0,2)2;
г) (1,1 + p)2; д) (1/2 α + 2/3 b)2; е) (3/4 x + 1/5 y)2;
ж) (0,2m + 2,1n)2; з) (0,4p + 0,3q)2; и) (3/5 αb + 1/2 c2)2.
а) (1/2 + α)2 = (1/2)2 + 2•1/2 α + α2 = 1/4 + α + α2;
б) (x + 1/3)2 = x2 + 2•1/3 x + (1/3)2 = x2 + 2/3 x + 1/9;
в) (m + 0,2)2 = m2 + 2•0,2m + 0,22 = m2 + 0,4m + 0,04;
г) (1,1 + p)2 = 1,12 + 2•1,1p + p2 = 1,21 + 2,2p + p2;
д) (1/2 α + 2/3 b)2 = (1/2 α)2 + 2•1/2 α•2/3 b + (2/3 b)2 = 1/4 α2 + 2/3 αb + 4/9 b2;
е) (3/4 x + 1/5 y)2 = (3/4 x)2 + 2•3/4 x•1/5 y + (1/5 y)2 = 9/16 x2 + 3/10 xy + 1/25 y2;
ж) (0,2m + 2,1n)2 = (0,2m)2 + 2•0,2m•2,1n + (2,1n)2 = 0,04m2 + 0,84mn + 4,41n2;
з) (0,4p + 0,3q)2 = (0,4p)2 + 2•0,4p•0,3q + (0,3q)2 = 0,16p2 + 0,24pq + 0,09q2;
и) (3/5 αb + 1/2 c2)2 = (3/5 αb)2 + 2•3/5 αb•1/2 c2 + (1/2c2)2 = 9/25 α2b2 + 3/5 αbc2 + 1/4 c4.
342. Доказываем. Пользуясь рисунком 13, докажите, что для α > 0, b > 0 верно равенство (α + b)(α + b) = α2 + 2αb + b2.
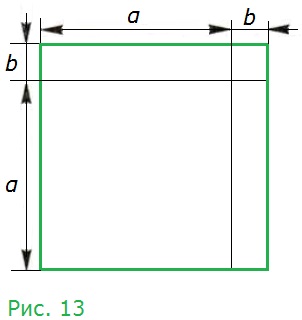
(α + b) − длина стороны всего квадрата, (α + b)(α + b) − площадь всего квадрата.
Площадь всего квадрата равна сумме площадей, входящих в него фигур: большой квадрат, малый квадрат и два прямоугольника.
α2 − площадь большого квадрата, b2 − площадь малого квадрата, αb − площадь каждого из двух прямоугольников.
Тогда: (α + b)(α + b) = α2 + b2 + αb + αb = α2 + 2αb + b2.
343. Вычислите, применив формулу квадрата суммы:
а) 412; б) 912; в) 2012;
г) 322; д) 722; е) 3022.
а) 412 = (40 + 1)2 = 402 + 2•40•1 + 12 = 1600 + 80 + 1 = 1681;
б) 912 = (90 + 1)2 = 902 + 2•90•1 + 12 = 8100 + 180 + 1 = 8281;
в) 2012 = (200 + 1)2 = 2002 + 2•200•1 + 12 = 40000 + 400 + 1 = 40401;
г) 322 = (30 + 2)2 = 302 + 2•30•2 + 22 = 900 + 120 + 4 = 1024;
д)722 = (70 + 2)2 = 702 + 2•70•2 + 22 = 4900 + 280 + 4 = 5184;
е) 3022 = (300 + 2)2 = 3002 + 2•300•2 + 22 = 90 000 + 1200 + 4 = 91 204.
344. Доказываем. Любое натуральное число, оканчивающееся цифрой 5, можно записать в виде 10α + 5.
Например: 25 = 10 • 2 + 5.
Докажите, что для вычисления квадрата такого числа можно к произведению α(α + 1) приписать справа 25.
Например: 252 = 625 (2 • 3 = 6).
Если α > 0 и α целое число то 10α заканчиваться цифрой 0, а если к нему прибавить 5, то оно будет заканчиваться цифрой 5.
(10α + 5)2 = (10α)2 + 2•10α•5 + 52 = 100α2 + 100α + 25 = 100α(α + 1) + 25 = 100•α(α + 1) + 25. Если α(α + 1) умножить на 100, то в конце полученного числа будут два нуля, которые заменятся на 25 при прибавлении 25. То есть к произведению α(α + 1) можно справа приписать число 25.
Например, 15 = 10•1 + 5, при α = 1 будет: 152 = 1(1 + 1) и 25 или 225.
Вообще для вычисления квадрата любого числа, заканчивающегося числом 5, α принимает значение из этого же числа, у которого убрали число 5 в конце. Например, 1015: убираем 5 и получаем 101 — это α. Теперь по формуле α(α + 1) и 25 получим: 101(101 + 1) и 25 = 101•102 и 25 = 10302 и 25 = 1030225 – это и есть 10152.
345. Представьте многочлен в виде квадрата суммы:
а) x2 + 2xy + y2; б) α2 + 4αb + 4b2;
в) 9m2 + 6mn + n2; г) 16p2 + 40pq + 25q2;
д) x2 + 2x + 1; е) 9 + 6α + α2;
ж) 16 + 8p + p2; з) 4m2 + 9n2 + 12mn;
и) x4 + 2x2y3 + y6; к) α6 + 2α3b3 + b6.
а) x2 + 2xy + y2 = (x + y)2;
б) α2 + 4αb + 4b2 = α2 + 2•α•2b + (2b)2 = (α + 2b)2;
в) 9m2 + 6mn + n2 = (3m)2 + 2•3m•n + n2 = (3m + n)2;
г) 16p2 + 40pq + 25q2 = (4p)2 + 2•4p•5q + (5q)2 = (4p + 5q)2;
д) x2 + 2x + 1 = (x + 1)2;
е) 9 + 6α + α2 = 32 + 2•3•α + α2 = (3 + α)2;
ж) 16 + 8p + p2 = 42 + 2•4•p + p2 = (4 + p)2;
з) 4m2 + 9n2 + 12mn = 4m2 + 12mn + 9n2 = (2m)2 + 2•2m•3n + (3n)2 = (2m + 3n)2;
и) x4 + 2x2y3 + y6 = (x2)2 + 2•x2•y3 + (y3)2 = (x2 + y3)2;
к) α6 + 2α3b3 + b6 = (α3)2 + 2•α3•b3 + (b3)2 = (α3 + b3)2.
346. Вместо букв C и D подберите одночлены так, чтобы выполнялось равенство:
а) (α + C)2 = D + 2αb + b2;
б) (2x + C)2 = 4x2 + 4xy + y2;
в) (C + 3m)2 = 4n2 + 12mn + 9m2;
г) (C + D)2 = 9p2 + 30pq + 25q2.
а) (α + C)2 = D + 2αb + b2
D = α2 C2 = b2
C = b
б) (2x + C)2 = 4x2 + 4xy + y2
C2 = y2
C = y
в) (C + 3m)2 = 4n2 + 12mn + 9m2
C2 = 4n2
C2 = (2n)2
C = 2n
г) (C + D)2 = 9p2 + 30pq + 25q2
C2 = 9p2 D2 = 25q2
C2 = (3p)2 D2 = (5q)2
C = 3p D = 5q
347. Преобразуйте выражение в многочлен стандартного вида:
а) (α + b)2 + (α + b)(α − b); б) (α + 3)2 + (x + 1)2;
в) 2(m + 1)2 + 3(m + 2)2; г) 5(p + q)2 + 3(p + 2q)2;
д) (2α + 3b)2 − (3α + 2b)2;
е) 2(3x + y)2 − 3(2x + 3y)2;
ж) (m + n)2 + 2(m + n)(2m − n) + (2m − n)2;
з) 2(p + 3q)(p + 2q) − (p + 2q)2 − (3q + p)2.
а) (α + b)2 + (α + b)(α − b) = (α + b)(α + b) + (α + b)(α − b) = (α + b)(α + b + α − b) = (α + b)2α = 2α2 + 2αb;
б) (α + 3)2 + (x + 1)2 = α2 + 6α + 9 + x2 + 2x + 1 = α2 + x2 + 6α + 2x + 10;
в) 2(m + 1)2 + 3(m + 2)2 = 2(m2 + 2m + 1) + 3(m2 + 4m + 4) = 2m2 + 4m + 2 + 3m2 + 12m + 12 = 5m2 + 16m + 14;
г) 5(p + q)2 + 3(p + 2q)2 = 5(p2 + 2pq + q2) + 3(p2 + 4pq + 4q2) = 5p2 + 10pq + 5q2 + 3p2 + 12pq + 12q2 = 8p2 + 22pq + 17q2;
д) (2α + 3b)2 − (3α + 2b)2 = 4α2 + 12αb + 9b2 − (9α2 + 12αb + 4b2) = 4α2 + 12αb + 9b2 − 9α2 − 12αb − 4b2 = −5α2 + 5b2;
е) 2(3x + y)2 − 3(2x + 3y)2 = 2(9x2 + 6xy + y2) − 3(4x2 + 12xy + 9y2) = 18x2 + 12xy + 2y2 − 12x2 − 36xy − 27y2 = 6x2 − 24xy − 25y2;
ж) (m + n)2 + 2(m + n)(2m − n) + (2m − n)2 = m2 + 2mn + n2 + 2(2m2 + 2mn – mn − n2) + 4m2 − 4mn + n2 = m2 + 2mn + n2 + 2(2m2 + mn − n2) + 4m2 − 4mn + n2 = m2 + 2mn + n2 + 4m2 + 2mn − 2n2 + 4m2 − 4mn + n2 = 9m2;
з) 2(p + 3q)(p + 2q) − (p + 2q)2 − (3q + p)2 = 2(p2 + 3pq + 2pq + 6q2) − (p2 + 4pq + 4q2) − (9q2 + 6pq + p2) = 2p2 + 6pq + 4pq + 12q2 − p2 − 4pq − 4q2 − 9q2 − 6pq − p2 = −q2.
| ← Предыдущая | Следующая → |