Начальные геометрические сведения
Измерение углов
Градусная мера угла. Измерение углов на местности
Ответы к стр. 20
Задачи
45. Градусные меры двух углов равны. Равны ли сами углы?
Да, так как равные углы имеют равные градусные меры.
46. На рисунке 37 изображены лучи с общим началом О.
а) Найдите градусные меры углов АОХ, BOX, АОВ, СОВ, DOX;
б) назовите углы, равные 20°;
в) назовите равные углы;
г) назовите все углы со стороной ОА и найдите их градусные меры.
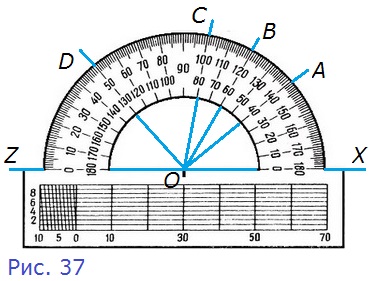
а) ∠АОХ = 40°, ∠BOX = 60°, ∠АОВ = 20° (60° — 40°), ∠СОВ = 20° (80° — 60°), ∠DOX = 130°;
б) ∠АОВ = 20°, ∠СОВ = 20°;
в) ∠XOA = ∠AOC = 40°, ∠COD = ∠DOZ = 50°, ∠АOB = ∠BOC = 20°;
г) ∠XOA = 40°, ∠AOB = 20°, ∠AOC = 40°, ∠AOD =90°, ∠AOZ = 140°.
47. Луч ОЕ делит угол АОВ на два угла. Найдите ∠AOB, если:
a) ∠AOE = 44°, ∠EOB = 77°;
б) ∠AOE = 12°37′, ∠EOB = 108°25′.
Р е щ е н и е
а) ∠АОВ = ∠АОЕ + ∠ЕОВ = 44° + 77° = 121°;
б) ∠АОВ = ∠АОЕ + ∠ЕОВ = 12°37′ + 108°25′ = 121°2′ (37′ + 25′ = 62′ = 1°2′).
О т в е т. а) ∠АОВ = 121°, б) ∠АОВ = 121°2′.
48. Луч ОС делит угол АОВ на два угла. Найдите угол СОВ, если ∠AOB = 78°, а угол АОС на 18° меньше угла BОС.
Р е ш е н и е
∠АОВ = ∠АОС + ∠СОВ, ∠АОС = ∠СОВ — 18°, тогда:
∠СОВ = ∠АОВ — ∠АОС,
∠СОВ = 78° — (∠СОВ — 18°),
∠СОВ = 78° — ∠СОВ + 18°,
2∠СОВ = 96°,
∠СОВ = 48°.
О т в е т. ∠СОВ = 48°.
49. Луч ОС делит угол АОВ на два угла. Найдите угол АОС, если ∠AOB = 155°, а угол АОС на 15° больше угла СОB.
Р е ш е н и е
∠АОВ = ∠АОС + ∠СОВ, ∠СОВ + 15° = ∠АОС ⇒ ∠СОВ = ∠АОС — 15°, тогда:
∠АОС = ∠АОВ — ∠СОВ,
∠АОС = 155° — (∠АОС — 15°),
∠АОС = 155° — ∠АОС + 15°,
2∠АОС = 170°,
∠АОС = 85°.
О т в е т. ∠АОС = 85°.
50. Угол АОВ является частью угла АОС. Известно, что ∠AOC = 108°, ∠AOB = 3∠BOC. Найдите угол АОВ.
Р е ш е н и е
∠АОС = ∠АОВ + ∠ВОС, ∠АОВ = 3∠ВОС ⇒ ∠ВОС = 1/3 ∠АОВ, тогда:
∠АОВ = ∠АОС — ∠ВОС,
∠АОВ = 108° — 1/3 ∠АОВ,
∠АОВ + 1/3 ∠АОВ = 108°,
4/3 ∠АОС = 108°,
∠АОС = 108° • 3/4,
∠АОС = 81°.
О т в е т. ∠АОС = 81°.
51. На рисунке 38 угол AOD — прямой, ∠AOB = ∠BOC = ∠COD. Найдите угол, образованный биссектрисами углов АОВ и COD.
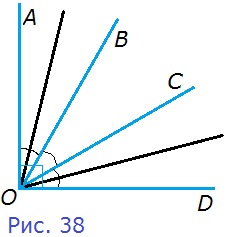
Р е ш е н и е
∠AOB = ∠BOC = ∠COD = 1/3 ∠АОD = 1/3 • 90° = 30°
Искомый угол равен сумме 1/2 ∠АОВ, ∠ВОС и 1/2 ∠СОD, так как биссектрисы делят угол пополам.
1/2 ∠АОВ + ∠ВОС + 1/2 ∠СОD = 1/2 • 30° + 30° + 1/2 • 30° = 60°.
О т в е т. Угол между биссектрисами углов АОВ и CОD 60°.
52. На рисунке 39 луч OV является биссектрисой угла ZOY, а луч OU — биссектрисой угла XOY. Найдите угол XOZ, если ∠UOV = 80°.
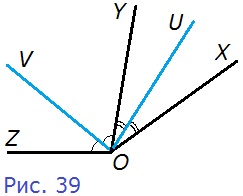
Р е ш е н и е
∠ХOZ = ∠ZOY + ∠XOY = ∠ZOV + ∠VOY + ∠YOU + ∠UOX
∠UOV = ∠VOY + ∠YOU, так как ∠ZOV = ∠VOY и ∠YOU = ∠UOX, тогда:
∠ZOV + ∠VOY + ∠YOU + ∠UOX = (∠VOY + ∠YOU) + (∠ZOV + ∠UOX) = 2∠UOV = 2 • 80° = 160°
О т в е т. ∠ХOZ = 160°.
53. Луч l является биссектрисой неразвёрнутого угла hk. Может ли угол hl быть прямым или тупым?
Р е ш е н и е
∠hk = ∠hl + ∠lk, ∠hl = ∠lk ⇒ ∠hk = 2∠hl
Если ∠hl прямой или тупой, то его градусная мера больше или равна 90°, то есть ∠hk больше или равен 180° (2 • 90°) — а это противоречит условию задачи: ∠hk неразвёрнутый (меньше 180°).
О т в е т. Не может.
| ← Предыдущая | Следующая → |