Начальные геометрические сведения
Перпендикулярные прямые
Смежные и вертикальные углы. Перпендикулярные прямые. Построение прямых углов на местности
Ответы к стр. 24
Практические задания
54. Начертите острый угол АОВ и на продолжении луча ОВ отметьте точку D. Сравните углы АОВ и AOD.
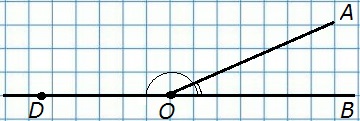
Углы АОВ и АОD — смежные, ∠АОВ — острый, ∠АОD — тупой ⇒ ∠АОВ < ∠АОD.
55. Начертите три угла: острый, прямой и тупой. Для каждого из них начертите смежный угол.
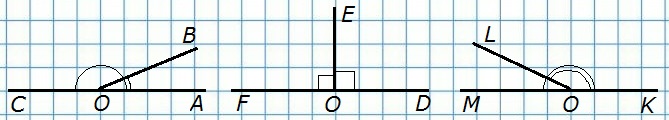
∠АОВ — острый, смежный угол ВОС (тупой).
∠DOE — прямой, смежный угол EOF (прямой).
∠KОL — тупой, смежный угол LOM (острый).
56. Начертите неразвернутый угол hk. Постройте угол h1k1 так, чтобы углы hk и h1k1 были вертикальными.
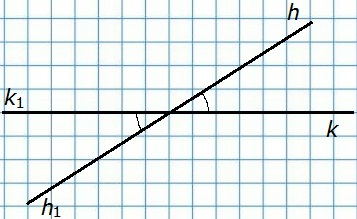
Углы hk и h1k1 — вертикальные (∠hk = ∠h1k1).
57. Начертите неразвернутый угол MON и отметьте точку Р внутри угла и точку Q — вне его. С помощью чертежного угольника и линейки через точки Р и Q проведите прямые, перпендикулярные к прямым ОМ и ON.
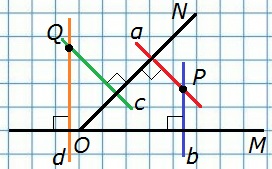
α ⊥ ОN, b ⊥ OM, c ⊥ ON, d ⊥ OM.
Задачи
58. Найдите угол, смежный с углом ABC, если: a) ∠ABC = 111°; б) ∠ABC = 90°; в) ∠ABC = 15°.
Р е ш е н и е
Сумма смежных углов равна 180°.
а) 180° — 111° = 69°;
б) 180° — 90° = 90°;
в) 180° — 15° = 165°.
О т в е т. а) 69°, б) 90°, в) 165°.
59. Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?
Р е ш е н и е
Сумма смежных углов равна 180°.
180° — 90° = 90° — прямой смежный угол.
О т в е т. Прямой.
60. Верно ли утверждение: если смежные углы равны, то они прямые?
Р е ш е н и е
Сумма смежных углов равна 180°.
180° : 2 = 90° — два смежных угла по 90° каждый.
О т в е т. Верно.
61. Найдите смежные углы hk и kl, если:
a) ∠hk меньше ∠kl на 40°;
б) ∠hk больше ∠kl на 120°;
в) ∠hk больше ∠kl на 47°18′;
г) ∠hk = 3∠kl;
д) ∠hk : ∠kl = 5 : 4.
Р е ш е н и е
Сумма смежных углов равна 180°.
а) ∠hk + ∠kl = 180°, ∠hk = ∠kl — 40°, тогда:
(∠kl — 40°) + ∠kl = 180°,
2∠kl = 180° + 40°,
∠kl = 220° : 2,
∠kl = 110°
∠hk = ∠kl — 40° = 110° — 40° = 70°
б) ∠hk + ∠kl = 180°, ∠hk = ∠kl + 120°, тогда:
(∠kl + 120°) + ∠kl = 180°,
2∠kl = 180° — 120°,
∠kl = 60° : 2,
∠kl = 30°
∠hk = ∠kl + 120° = 30° + 120° = 150°
в) ∠hk + ∠kl = 180°, ∠hk = ∠kl + 47°18′, тогда:
(∠kl + 47°18′) + ∠kl = 180°,
2∠kl = 180° — 47°18′,
∠kl = 132°42′ : 2,
∠kl = 66°21′
∠hk = ∠kl + 47°18′ = 66°21′ + 47°18′ = 113°39′
г) ∠hk + ∠kl = 180°, ∠hk = 3∠kl, тогда:
3∠kl + ∠kl = 180°,
4∠kl = 180°,
∠kl = 180° : 4,
∠kl = 45°
∠hk = 3∠kl = 3 • 45° = 135°
д) ∠hk + ∠kl = 180°, ∠hk : ∠kl = 5 : 4 или ∠hk : ∠kl = 5/4 ⇒ ∠hk = 5/4 • ∠kl, тогда:
5/4 ∠kl + ∠kl = 180°,
9/4 ∠kl = 180°,
∠kl = 180° : 9/4,
∠kl = 180° • 4/9,
∠kl = 80°
∠hk = 5/4 ∠kl = 5/4 • 80° = 100°
О т в е т. а) ∠kl = 110°, ∠hk = 70°;
б) ∠kl = 30°, ∠hk = 150°;
в) ∠kl = 66°21′, ∠hk = 113°39′;
г) ∠kl = 45°, ∠hk = 135°;
д) ∠kl = 80°, ∠hk = 100°.
62. На рисунке 46 углы BOD и COD равны. Найдите угол AOD, если ∠COB = 148°.
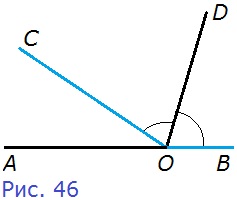
Р е ш е н и е
∠AOD = ∠AOC + ∠COD
Углы AOC и COB — смежные, тогда:
∠AOC + ∠COB = 180° ⇒ ∠АОС = 180° — ∠СОВ = 180° — 148° = 32°.
∠СОВ = ∠СОD + ∠DOB = 148°, ∠СОD = ∠DOB ⇒ ∠СОD = 148° : 2 = 74°.
∠AOD = 32° + 74° = 106°.
О т в е т. ∠AOD = 106°.
63. Даны два равных угла. Равны ли смежные с ними углы?
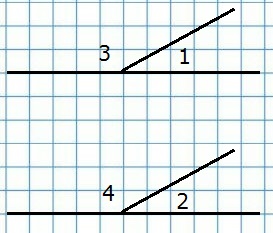
Р е ш е н и е
∠1 = ∠2
∠1 + ∠3 = 180° ⇒ ∠3 = 180° — ∠1
∠2 + ∠4 = 180° ⇒ ∠4 = 180° — ∠2
Так как ∠1 = ∠2, то ∠3 = 180° — ∠1 = 180° — ∠2 = ∠4 или
∠4 = 180° — ∠2 = 180° — ∠1 = ∠3
О т в е т. Равны.
64. Найдите изображенные на рисунке 41 углы:
а) 1, 3, 4, если ∠2 = 117°;
б) 1, 2, 4, если ∠3 = 43°27′.
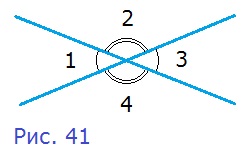
Р е ш е н и е
а) Углы 2 и 4 — вертикальные, тогда ∠2 = ∠4 = 117°
Углы 1 и 2 — смежные, тогда ∠1 + ∠2 = 180° ⇒ ∠1 = 180° — ∠2 = 180° — 117° = 63°
Углы 1 и 3 — вертикальные, тогда ∠1 = ∠3 = 63°
б) Углы 1 и 3 — вертикальные, тогда ∠1 = ∠3 = 43°27′
Углы 1 и 2 — смежные, тогда ∠1 + ∠2 = 180° ⇒ ∠2 = 180° — ∠1 = 180° — 43°27′ = 136°33′
Углы 2 и 4 — вертикальные, тогда ∠2 = ∠4 = 136°33′
О т в е т. а) ∠1 = ∠3 = 63°, ∠4 = 117°; б) ∠1 = 43°27′, ∠2 = ∠4 = 136°33′.
| ← Предыдущая | Следующая → |