Параллельные прямые
Признаки параллельности двух прямых
Определение параллельных прямых. Признаки параллельности двух прямых. Практические способы построения параллельных прямых
Ответы к стр. 56
Задачи
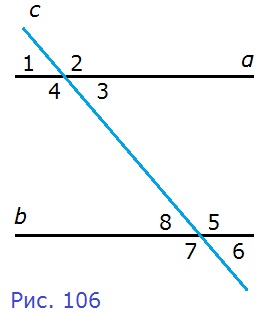
186. На рисунке 106 прямые α и b пересечены прямой с. Докажите, что α||b, если:
a) ∠1 = 37°, ∠7 = 143°;
б) ∠1 = ∠6;
в) ∠1 = 45°, а угол 7 в три раза больше угла 3.
Д а н о
с ∩ α
с ∩ b
a) ∠1 = 37°, ∠7 = 143°
б) ∠1 = ∠6
в) ∠1 = 45°, а угол 7 в три раза больше угла 3
Д о к а з а т ь
α||b
Д о к а з а т е л ь с т в о
а) ∠1 = ∠3 = 37° — так как они вертикальные
∠7 = ∠5 = 143° — так как они вертикальные
∠3 и ∠5 – односторонние углы, ∠3 + ∠5 = 37° + 143° = 180° — следовательно, α||b, ЧТД (что и требовалось доказать).
б) ∠1 = ∠3 — так как они вертикальные
∠6 = ∠8 — так как они вертикальные
∠3 и ∠8 – накрест лежащие углы, ∠3 = ∠8 — следовательно, α||b, ЧТД (что и требовалось доказать).
в) ∠1 = ∠3 = 45° — так как они вертикальные
∠7 = 3∠3 = 3•45° = 135°
∠7 = ∠5 = 135° — так как они вертикальные
∠3 и ∠5 – односторонние углы, ∠3 + ∠5 = 45° + 135° = 180° — следовательно, α||b, ЧТД (что и требовалось доказать).
О т в е т: α||b.
187. По данным рисунка 107 докажите, что AB||DE.
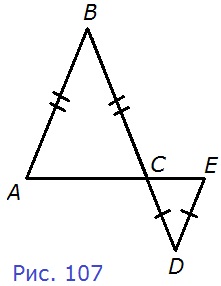
Д а н о
ΔАВС, АВ = ВС
ΔCDE, CD = DE
Д о к а з а т ь
AB||DE
Д о к а з а т е л ь с т в о
Так как АВ = ВС, то ΔАВС — равнобедренный, следовательно ∠BАC = ∠AСB.
Так как CD = DE, то ΔCDE — равнобедренный, следовательно ∠EСD = ∠DEC.
∠AСB = ∠EСD — так как они вертикальные, следовательно, ∠BАC = ∠AСB = ∠EСD = ∠DEC.
∠BАC и ∠DEC – накрест лежащие углы при пересечении прямой АЕ прямых AB и DE, следовательно, AB||DE, так как ∠BАC = ∠DEC, ЧТД (что и требовалось доказать).
О т в е т: AB||DE.
188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АС и BD параллельны.
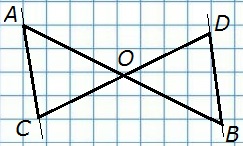
Д а н о
АВ ∩ CD
т. О — середина АВ и CD
Д о к а з а т ь
AС||ВD
Д о к а з а т е л ь с т в о
Точка О — середина АВ и CD, значит АO = OВ, СО = OD — по условию. ∠АОС = ∠DOB, т. к. вертикальные. Следовательно, ΔАОС = ΔDOB по первому признаку равенства треугольников (по двум сторонам и углу между ними). ∠АCO и ∠ODB – накрест лежащие углы при пересечении прямой СD прямых AC и BD, следовательно, AС||ВD, так как ∠АCO = ∠ODB, ЧТД (что и требовалось доказать).
О т в е т: AС||ВD.
189. Используя данные рисунка 108, докажите, что BC||AD.
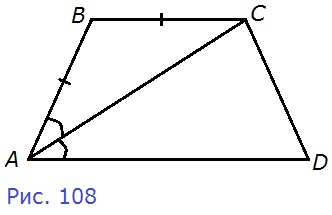
Д а н о
АВ = ВС
∠ВАС = ∠САD
Д о к а з а т ь
BC||AD
Д о к а з а т е л ь с т в о
АВ = ВС (по условию), следовательно, ΔАВС — равнобедренный. ∠ВАС = ∠BСА — как углы при основании равнобедренного треугольника. Тогда ∠ВАС = ∠САD. ∠САD и ∠BCA – накрест лежащие углы при пересечении прямой AС прямых BC и AD, следовательно, BC||AD, так как ∠САD = ∠BCA, ЧТД (что и требовалось доказать).
О т в е т: BC||AD.
190. На рисунке 109 АВ = BC, AD = DE, ∠C = 70°, ∠EAC = 35°. Докажите, что DE||АС.
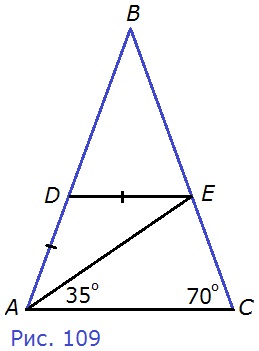
Д а н о
ΔАВС
АВ = АС
AD = DE
∠C = 70°
∠EAC = 35°
Д о к а з а т ь
DE||АС
Д о к а з а т е л ь с т в о
АВ = ВС (по условию), следовательно, ΔАВС — равнобедренный. ∠ВАС = ∠BСА — как углы при основании равнобедренного треугольника. Тогда ∠DАE = ∠ВАС : 2 = 70° : 2 = 35°. AD = DE (по условию), следовательно, ΔАDE — равнобедренный. ∠DАE = ∠DEА — как углы при основании равнобедренного треугольника. ∠DEA и ∠EAC – накрест лежащие углы при пересечении прямой AE прямых DE и AC, следовательно, DE||АС, так как ∠DEA = ∠EAC, ЧТД (что и требовалось доказать).
О т в е т: DE||АС.
191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающая сторону ВС в точке М так, что ВМ = МК. Докажите, что КМ||АВ.
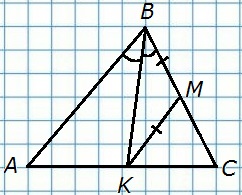
Д а н о
ΔАВС
ВК — биссектриса
ВМ = МК
Д о к а з а т ь
КМ||АВ
Д о к а з а т е л ь с т в о
Так как ВК — биссектриса, то ∠ABK = ∠CBK. ВМ = МК (по условию), следовательно, ΔВMK — равнобедренный. ∠MВK = ∠BKM — как углы при основании равнобедренного треугольника. Тогда ∠АBK = ∠BKM. ∠АBK и ∠BKM – накрест лежащие углы при пересечении прямой BK прямых AB и KM, следовательно, КМ||АВ, так как ∠АBK = ∠BKM, ЧТД (что и требовалось доказать).
О т в е т: КМ||АВ.
192. В треугольнике ABC угол А равен 40°, а угол BCE, смежный с углом ACB, равен 80°. Докажите, что биссектриса угла ВСЕ параллельна прямой АВ.
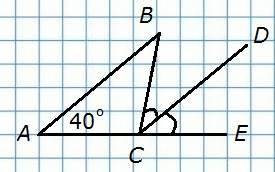
Д а н о
ΔАВС
∠A = 40°
∠BCE = 80°
CD — биссектриса ∠BCE
Д о к а з а т ь
CD||АВ
Д о к а з а т е л ь с т в о
Так как CD — биссектриса, то ∠BCD = ∠DCE = 80° : 2 = 40°. ∠ВАС и ∠DCE – соответственные углы при пересечении прямой АЕ прямых AB и СD, следовательно, CD||АВ, так как ∠ВАС = ∠DCE, ЧТД (что и требовалось доказать).
О т в е т: CD||АВ.
193. В треугольнике ABC ∠A = 40°, ∠B = 70°. Через вершину B проведена прямая BD так, что луч ВС — биссектриса угла ABD. Докажите, что AC||BD.
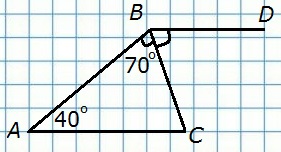
Д а н о
ΔАВС
∠A = 40°
∠B = 70°
BD — биссектриса ∠ABD
Д о к а з а т ь
AC||BD
Д о к а з а т е л ь с т в о
Так как BС — биссектриса, то ∠АBD = 2∠АВC = 2•70° = 140°. ∠ВАС и ∠АВD – внутренние односторонние углы при пересечении прямой АВ прямых AС и ВD, следовательно, AC||BD, так как ∠ВАС + ∠АВD = 40° + 140° = 180°, ЧТД (что и требовалось доказать).
О т в е т: AC||BD.
194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертёжного угольника и линейки проведите прямую, параллельную противоположной стороне.
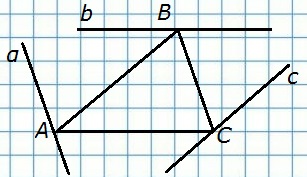
Способ построения подробно описан в п. 26 на стр. 55 учебника, второй абзац.
195. Начертите треугольник ABC и отметьте точку D на стороне АС. Через точку D с помощью чертежного угольника и линейки проведите прямые, параллельные двум другим сторонам треугольника.
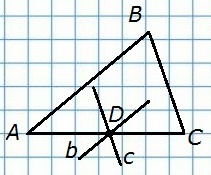
Способ построения подробно описан в п. 26 на стр. 55 учебника, второй абзац.
| ← Предыдущая | Следующая → |