Параллельные прямые
Аксиома параллельных прямых
Об аксиомах геометрии. Аксиома параллельных прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей. Углы с соответственно параллельными или перпендикулярным сторонами
Ответы к стр. 65
Задачи
196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провести через вершину С?
По аксиоме параллельных прямых через точку (вершину С), не лежащую на данной прямой (стороне АВ), можно провести только одну прямую, параллельную данной.
197. Через точку, не лежащую на прямой р, проведены четыре прямые. Сколько из этих прямых пересекают прямую р? Рассмотрите все возможные случаи.
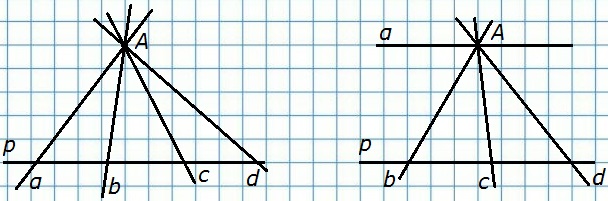
Возможно два варианта: все прямые пересекают прямую р и три прямые пересекают прямую р, а одна ей параллельна (по аксиоме параллельных прямых через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной).
198. Прямые α и b перпендикулярны к прямой р, прямая с пересекает прямую α. Пересекает ли прямая с прямую b?
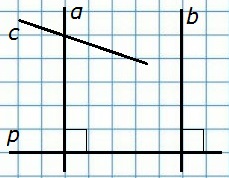
Две прямые, перпендикулярные к третьей, не пересекаются, то есть являются параллельными: α||b. Согласно следствию 1° из аксиомы параллельных прямых, если прямая (с) пересекает одну из двух параллельных прямых (α), то она пересекает и другую (b).
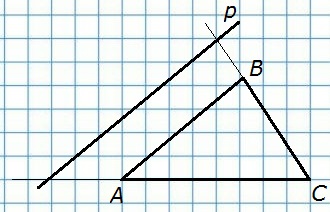
199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВС и АС пересекают прямую р.
Д а н о
ΔАВС
р||AВ
Д о к а з а т ь
ВС ∩ р
АС ∩ р
Д о к а з а т е л ь с и в о
ВС ∩ АВ в т. В. Согласно следствию 1° из аксиомы параллельных прямых, если прямая (ВС) пересекает одну из двух параллельных прямых (АВ), то она пересекает и другую (р).
АС ∩ АВ в т. А. Согласно следствию 1° из аксиомы параллельных прямых, если прямая (АС) пересекает одну из двух параллельных прямых (ВС), то она пересекает и другую (р).
О т в е т: ВС ∩ р, АС ∩ р.
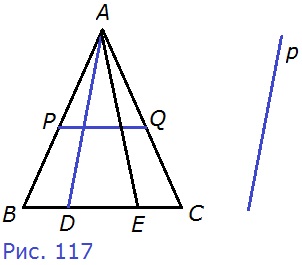
200. На рисунке 115 AD||p и PQ||BC. Докажите, что прямая р пересекает прямые АВ, АЕ, АС, ВС и PQ.
Д а н о
AD||p
PQ||BC
Д о к а з а т ь
р ∩ АВ, АЕ, АС, ВС и PQ
Д о к а з а т е л ь с т в о
АD ∩ АВ, АЕ, АС в т. А, АD ∩ ВС и PQ. AD||p (по условию), следовательно, согласно следствию 1° из аксиомы параллельных прямых, если прямая (АВ, АЕ, АС, ВС и PQ) пересекает одну из двух параллельных прямых (АD), то она пересекает и другую (р).
О т в е т: р ∩ АВ, АЕ, АС, ВС и PQ.
201. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210°. Найдите эти углы.
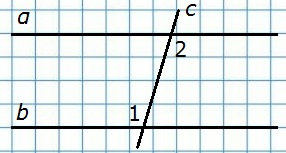
Д а н о
α||b
∠1 + ∠2 = 210°
Н а й т и
∠1 — ?
∠2 — ?
Р е ш е н и е
∠1 и ∠2 – накрест лежащие углы при прямых α и b и секущей с, следовательно, ∠1 = ∠2 = 210° : 2 = 105°.
О т в е т: ∠1 = ∠2 = 105°.
202. На рисунке 118 прямые α, b и с пересечены прямой d, ∠1 = 42°, ∠2 = 140°, ∠3 = 138°. Какие из прямых α, b и с параллельны?
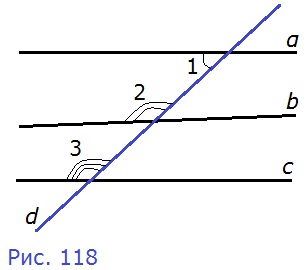
Д а н о
а, b и с ∩ d
∠1 = 42°
∠2 = 140°
∠3 = 138°
Н а й т и
параллельные прямые
Р е ш е н и е
1) ∠1 и ∠2 — внутренние односторонние при прямых α и b и секущей d, следовательно, ∠1 + ∠2 = 42° + 142° = 182°, но ∠1 + ∠2 ≠ 180°, значит, α∦b.
2) ∠1 и ∠3 — внутренние односторонние при прямых α и с и секущей d, следовательно, ∠1 + ∠3 = 42° + 138° = 180°, значит, α||с.
3) ∠2 и ∠3 — соответственные при прямых b и с и секущей d, следовательно, ∠2 = ∠3, но ∠2 (140°) ≠ ∠3 (138°), значит, b∦с.
О т в е т: α||с.
203. Найдите все углы, образованные при пересечении двух параллельных прямых α и b секущей с, если:
а) один из углов равен 150°;
б) один из углов на 70° больше другого.
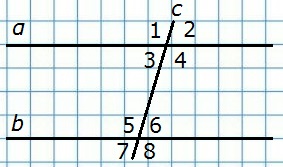
Д а н о
α||b
а) ∠1 = 150°
б) ∠1 = ∠2 + 70°
Н а й т и
все углы
Р е ш е н и е
а) ∠1 и ∠4 — вертикальные, следовательно, ∠1 = ∠4. ∠4 и ∠5 – накрест лежащие углы при прямых α и b и секущей с, следовательно, ∠4 = ∠5. ∠5 и ∠8 — вертикальные, следовательно, ∠5 = ∠8. Тогда ∠1 = ∠4 = ∠5 = ∠8 = 150°.
∠1 и ∠2 — смежные, следовательно, ∠2 = 180° — ∠1 = 180° — 150° = 30°. ∠2 и ∠3 — вертикальные, следовательно, ∠2 = ∠3. ∠3 и ∠6 – накрест лежащие углы при прямых α и b и секущей с, следовательно, ∠3 = ∠6. ∠6 и ∠7 — вертикальные, следовательно, ∠6 = ∠7. Тогда ∠2 = ∠3 = ∠6 = ∠7 = 30°.
б) ∠1 и ∠2 — смежные, следовательно, ∠1 + ∠2 = 180° и ∠1 = ∠2 + 70°, тогда ∠2 + 70° + ∠2 = 180° или 2∠2 = 110° или ∠2 = 55°, а ∠1 = ∠2 + 70° = 55° + 70° = 125°.
∠1 и ∠4 — вертикальные, следовательно, ∠1 = ∠4. ∠4 и ∠5 – накрест лежащие углы при прямых α и b и секущей с, следовательно, ∠4 = ∠5. ∠5 и ∠8 — вертикальные, следовательно, ∠5 = ∠8. Тогда ∠1 = ∠4 = ∠5 = ∠8 = 125°.
∠2 и ∠3 — вертикальные, следовательно, ∠2 = ∠3. ∠3 и ∠6 – накрест лежащие углы при прямых α и b и секущей с, следовательно, ∠3 = ∠6. ∠6 и ∠7 — вертикальные, следовательно, ∠6 = ∠7. Тогда ∠2 = ∠3 = ∠6 = ∠7 = 55°.
О т в е т: а) ∠1 = ∠4 = ∠5 = ∠8 = 150°, ∠2 = ∠3 = ∠6 = ∠7 = 30°; б) ∠1 = ∠4 = ∠5 = ∠8 = 125°, ∠2 = ∠3 = ∠6 = ∠7 = 55°.
204. Концы отрезка АВ лежат на параллельных прямых α и b. Прямая, проходящая через середину О этого отрезка, пересекает прямые α и b в точках С и D. Докажите, что CO = OD.
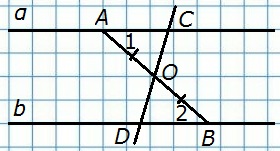
Д а н о
α||b
АО = ОB
Д о к а з а т ь
CO = OD
Д о к а з а т е л ь с т в о
АО = ОB (по условию), ∠АОС = ∠DOB (так как вертикальные), ∠1 = ∠2 – накрест лежащие углы при прямых α и b и секущей с, следовательно, ΔАОС = ΔDOB (по второму признаку равенства треугольников), значит CO = OD.
О т в е т: CO = OD.
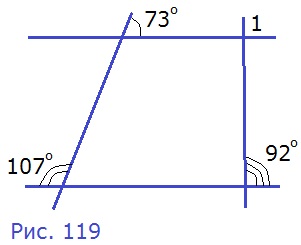
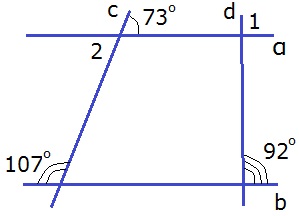
205. По данным рисунка 117 найдите ∠1.
Д а н о
рисунок
Н а й т и
∠1
Р е ш е н и е
Угол 73° и ∠2 — вертикальные, следовательно, ∠2 = 73°. ∠2 и угол 107° — внутренние односторонние при прямых α и b и секущей с, ∠2 + 107° = 73° + 107° = 180° — следовательно, α||b. Угол 92° и ∠1 — соответственные при параллельных прямых α и b и секущей d, следовательно, равные: ∠1 = 92°.
О т в е т: ∠1 = 92°.
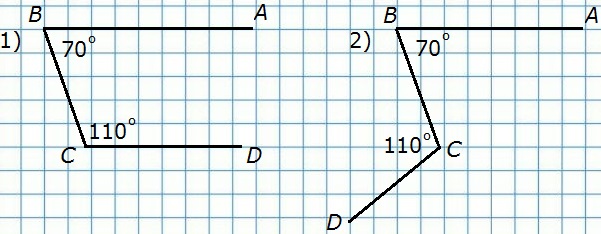
206. ∠ABC = 70°, а ∠BCD = 110°. Могут ли прямые АВ и CD быть:
а) параллельными;
б) пересекающимися?
Д а н о
∠ABC = 70°
∠BCD = 110°
Д о к а з а т ь
а) AB||CD
б) AB ∩ CD
Д о к а з а т е л ь с т в о
а) Рис. 1. ∠ABC и ∠BCD — внутренние односторонние при прямых АВ и CD и секущей ВС, ∠ABC + ∠BCD = 70° + 110° = 180°, следовательно, AB||CD.
б) Рис. 2. ∠ABC и ∠BCD — внутренние накрест лежащие при прямых АВ и CD и секущей ВС, ∠ABC (70°) ≠ ∠BCD (110°), следовательно, AB ∩ CD.
О т в е т: а) AB||CD, б) AB ∩ CD.
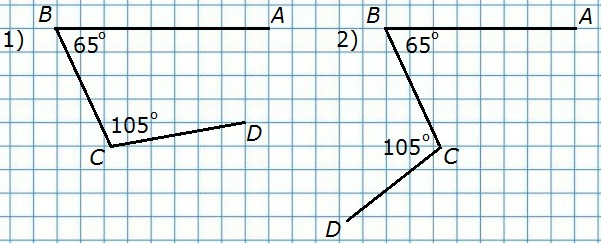
207. Ответьте на вопросы задачи 206, если ∠ABC = 65°, a ∠BCD = 105°.
Д а н о
∠ABC = 65°
∠BCD = 105°
Д о к а з а т ь
а) AB||CD
б) AB ∩ CD
Д о к а з а т е л ь с т в о
а) Рис. 1. ∠ABC и ∠BCD — внутренние односторонние при прямых АВ и CD и секущей ВС, ∠ABC + ∠BCD = 65° + 105° = 170°, следовательно, AB∦CD (AB ∩ CD).
б) Рис. 2. ∠ABC и ∠BCD — внутренние накрест лежащие при прямых АВ и CD и секущей ВС, ∠ABC (65°) ≠ ∠BCD (105°), следовательно, AB ∩ CD.
О т в е т: а) AB∦CD (AB ∩ CD), б) AB ∩ CD.
| ← Предыдущая | Следующая → |