Параллельные прямые
Аксиома параллельных прямых
Об аксиомах геометрии. Аксиома параллельных прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей. Углы с соответственно параллельными или перпендикулярным сторонами
Ответы к стр. 66
Задачи
208. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°. Найдите эти углы.
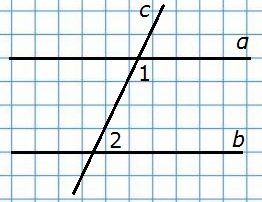
Д а н о
α||b
c — секущая
∠1 — ∠2 = 50°
Н а й т и
∠1 — ?
∠2 — ?
Р е ш е н и е
Так как ∠1 и ∠2 — односторонние при α||b и секущей с, то ∠1 + ∠2 = 180°. ∠1 — ∠2 = 50° ⇒ ∠1 = 50° + ∠2. Тогда ∠1 + ∠2 = 50° + ∠2 + ∠2 = 180° или 2∠2 = 130° или ∠2 = 65°, а ∠1 = 50° + ∠2 = 50° + 65° = 115°.
О т в е т: ∠1 = 115°, ∠2 = 65°.
209. На рисунке 120 α||b, c||d, ∠4 = 45°. Найдите углы 1, 2 и 3.
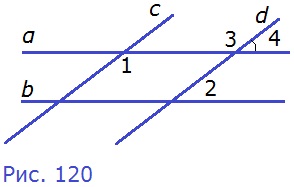
Д а н о
α||b
c||d
∠4 = 45°
Н а й т и
∠1 — ?
∠2 — ?
∠3 — ?
Р е ш е н и е
∠4 и ∠2 — соответственные углы при α||b и секущей d, значит ∠4 = ∠2 = 45°. ∠3 и ∠4 — смежные, значит ∠3 + ∠4 = 180° ⇒ ∠3 = 180° — ∠4 = 180° — 45° = 135°. ∠1 и ∠3 — внутренние накрест лежащие углы при c||d и секущей α, значит ∠1 = ∠3 = 135°.
О т в е т: ∠1 = 135°, ∠2 = 45°, ∠3 = 135°.
210. Два тела Р1 и Р2 подвешены на концах нити, перекинутой через блоки А и В (рис. 121). Третье тело Р3 подвешено на той же нити в точке С и уравновешивает тела Р1 и Р2. (При этом АР1||BР2||СР3.) Докажите, что ∠ACB = ∠CAP1 + ∠CBP2.
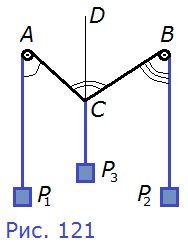
Д а н о
Рисунок
АР1||BР2||СР3
Д о к а з а т ь
∠ACB = ∠CAP1 + ∠CBP2
Д о к а з а т е л ь с и в о
Дополнительное построение: луч СD. ∠ACB = ∠ACD + ∠DCB. ∠CAP1 и ∠ACD — внутренние накрест лежащие углы при АР1||СР3 и секущей АС, значит ∠CAP1 = ∠ACD. ∠CBP2 и ∠DCB — внутренние накрест лежащие углы при СР3||ВР2 и секущей СВ, значит ∠CBP2 = ∠DCB. Тогда ∠ACB = ∠ACD + ∠DCB = ∠CAP1 + ∠CBP2.
О т в е т: ∠ACB = ∠CAP1 + ∠CBP2.
211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисы накрест лежащих углов параллельны; б) биссектрисы односторонних углов перпендикулярны.
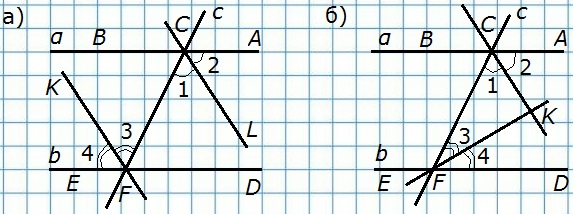
Д а н о
α||b
с — секущая
Д о к а з а т ь
а) KF||CL
б) KF⏊CK
Д о к а з а т е л ь с и в о
а) ∠ACF и ∠CFE — внутренние накрест лежащие углы при α||b и секущей c, значит ∠ACF = ∠CFE. ∠ACF = ∠1 + ∠2, ∠1 = ∠2, так как CL — биссектриса ∠ACF. ∠CFE = ∠3 + ∠4, ∠3 = ∠4, так как KF — биссектриса ∠CFE. Следовательно, ∠1 = ∠2 = ∠3 = ∠4. ∠3 и ∠1 — внутренние накрест лежащие углы при KF и CL и секущей CF, ∠3 = ∠1, значит KF||CL.
б) ∠ACF и ∠DFC — внутренние односторонние углы при α||b и секущей c, значит ∠ACF + ∠DFC = 180°. ∠ACF = ∠1 + ∠2, ∠1 = ∠2, так как CK — биссектриса ∠ACF. ∠DFC = ∠3 + ∠4, ∠3 = ∠4, так как KF — биссектриса ∠DFC. Рассмотрим ΔCFK: ∠KCF + ∠CFK + ∠FKC = ∠1 + ∠3 + ∠FKC = 180°. ∠1 + ∠3 = 1/2 ∠ACF + 1/2 ∠DFC = 1/2(∠ACF + ∠DFC) = 1/2•180° = 90°. Тогда ∠1 + ∠3 + ∠FKC = 90° + ∠FKC = 180° ⇒ ∠FKC = 180° — 90° = 90°. Так как ∠FKC = 90°, то KF⏊CK.
О т в е т: а) KF||CL, б) KF⏊CK
212. Прямые, содержащие высоты АА1 и ВВ1 треугольника АВС, пересекаются в точке Н, угол В — тупой, ∠С = 20°. Найдите угол АНВ.
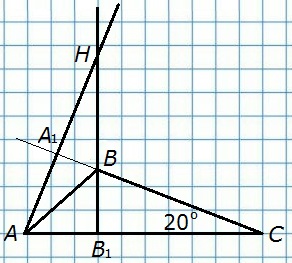
Д а н о
ΔAВС
АА1, ВВ1 — высота
АА1 ∩ ВВ1 в т. Н
∠С = 20°
∠В — тупой
Н а й т и
∠АНВ
Р е ш е н и е
Рассмотри ΔВВ1С: ∠ВВ1С = 90°, так как ВВ1 — высота к АС. Тогда ∠ВВ1С + ∠В1СВ + ∠СВВ1 = 180° ⇒ ∠СВВ1 = 180° — ∠ВВ1С — ∠В1СВ = 180° — 90° — 20° = 70°.
Рассмотрим ΔНВА1: ∠НА1В = 90°, так как АА1 — высота к ВС. ∠НВА1 = ∠СВВ1 = 70° — так как вертикальные. ∠АНВ = А1НВ. Тогда ∠НВА1 + ∠ВА1Н + ∠А1НВ = 180° ⇒ ∠А1НВ = 180° — ∠НВА1 — ∠НА1В = 180° — 70° — 90° = 20°.
О т в е т: ∠АНВ = 20°.
Вопросы для повторения к главе III
1. Дайте определение параллельных прямых. Какие два отрезка называются параллельными?
Две прямые на плоскости называются параллельными, если они не пересекаются. Два отрезка называются параллельными, если они лежат на параллельных прямых.
2. Что такое секущая по отношению к двум прямым? Назовите пары углов, которые образуются при пересечении двух прямых секущей.
Прямая с называется секущей по отношению к прямым α и b, если она пересекает их в двух точках.
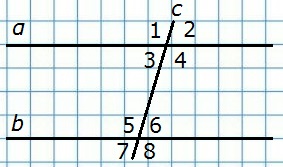
Внутренние накрест лежащие углы: 3 и 6, 4 и 5 — попарно равны.
Внешние накрест лежащие углы: 1 и 8, 2 и 7 — попарно равны.
Внутренние односторонние углы: 4 и 6, 3 и 5 — их сумма 180°.
Внешние односторонние углы: 1 и 7, 2 и 8 — их сумма 180°.
Соответственные углы: 1 и 5, 2 и 6, 3 и 7, 4 и 8 — попарно равны.
3. Докажите, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
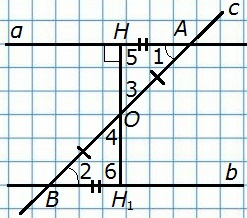
Д а н о
с ∩ α, с ∩ b
∠1 = ∠2
Д о к а з а т ь
α||b
Д о к а з а т е л ь с и в о
Из середины О отрезка АВ проведём перпендикуляр ОН к прямой α. На прямой b от точки В отложим отрезок ВН1, равный отрезку АН и проведём отрезок ОН1. Треугольники ОНА и ОН1В равны по двум сторонам и углу между ними (АО = ВО, АН = ВН1, ∠1 = ∠2), поэтому ∠3 = ∠4 и ∠5 = ∠6. Из равенства ∠3 = ∠4 следует, что точка Н1 лежит на продолжении луча ОН, то есть точки Н, О и Н1 лежат на одной прямой, а из равенства ∠5 = ∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Итак, прямые α и b перпендикулярны к прямой НН1, поэтому они параллельны.
О т в е т: α||b.
4. Докажите, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
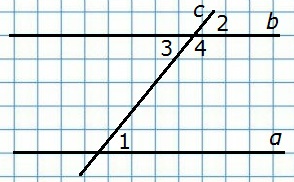
Д а н о
с ∩ α, с ∩ b
∠1 = ∠2
Д о к а з а т ь
α||b
Д о к а з а т е л ь с и в о
Так как углы 2 и 3 — вертикальные, то ∠2 = ∠3. Из этих двух равенств следует, что ∠1 = ∠3. Но углы 1 и 3 — накрест лежащие, поэтому прямые α и b параллельны.
О т в е т: α||b.
5. Докажите, что если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
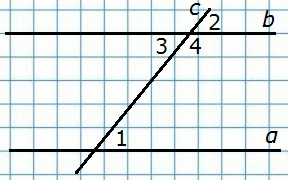
Д а н о
с ∩ α, с ∩ b
∠1 + ∠4 = 180°
Д о к а з а т ь
α||b
Д о к а з а т е л ь с и в о
Так как углы 3 и 4 — смежные, то ∠3 + ∠4 = 180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые α и b параллельны.
О т в е т: α||b.
6. Расскажите о практических способах проведения параллельных прямых.
На практике параллельные прямые проводят с помощью: чертёжного угольника и линейки, рейсшины (в чертёжной практике), малки (две деревянные планки, скреплённые шарниром) при столярных работах.
7. Объясните, какие утверждения называются аксиомами. Приведите примеры аксиом.
Аксиомы — утверждения о свойствах геометрических фигур, принимаемые в качестве исходных положений, на основе которых доказываются далее теоремы и вообще строится вся геометрия.
Через любые две точки проходит прямая, и притом только одна.
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
8. Докажите, что через данную точку, не лежащую на данной прямой, проходит прямая, параллельная данной.
Утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом и само является аксиомой.
9. Сформулируйте аксиому параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
10. Какое утверждение называется следствием? Докажите, что прямая, пересекающая одну из двух параллельных прямых, пересекает и другую.
Следствия — утверждения, которые выводятся непосредственно из аксиом или теорем.
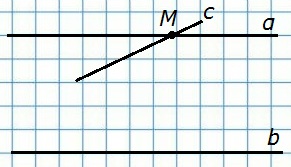
Пусть прямые α и b параллельны и прямая с пересекает прямую α в точке М. Если бы прямая с не пересекала прямую b, то через точку М проходили бы две прямые (прямые α и с), параллельные прямой b. Но это противоречит аксиоме параллельных прямых, и, значит, прямая с пересекает прямую b.
| ← Предыдущая | Следующая → |