Числа от 1 до 1000
Сложение и вычитание
Нахождение нескольких долей целого
Ответы к стр. 64
291. Начерти отрезок длиной 60 мм. Узнай, сколько миллиметров в пяти шестых долях этого отрезка.
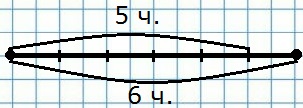
1) 60 : 6 = 10 (мм) − составляют одну шестую доли длины отрезка;
2) 10 • 5 = 50 (мм) − составляют пять шестых долей длины отрезка.
О т в е т: 50 мм.
292. Начерти такой прямоугольник. Вырежи его и разрежь по проведённому в нём отрезку. Проверь наложением, что полученные треугольники равны. Найди площадь одного треугольника.
Площадь одного треугольника будет равна половине площади прямоугольника. Стороны прямоугольника равны 30 мм и 50 мм.
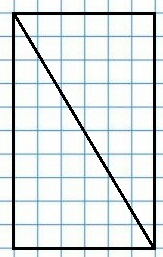
Sпрямоугольника = 30 • 50 = 1500 мм2;
SΔ = 1500 : 2 = 750 мм2.
293. За 7 дней в столовой израсходовали 21 кг масла. На сколько дней при той же норме расхода хватит 36 кг масла? На сколько дней хватило бы этого масла, если бы каждый день расходовали на 1 кг больше?
1) 21 : 7 = 3 (кг) − масла расходовали за 1 день;
2) 36 : 3 = 12 (д.) − хватит 36 кг масла;
3) 3 + 1 = 4 (кг) − масла расходовалось бы в день, если бы в день расходовали на 1 кг больше;
4) 36 : 4 = 9 (дней) − хватило бы масла, если бы в день расходовали 4 кг.
О т в е т: 36 кг масла при обычной норме расхода хватит на 12 дней; если бы каждый день расходовали масла на 1 кг больше, 36 кг масла хватило бы на 9 дней.
294.
231 • 4 = 924 984 : 8 = 123
304 • 3 = 912 938 : 7 = 134
129 • 6 = 774 876 : 4 = 219
752 : 2 − 540 : 9 − 48 • 6 = 28
(608 + 206) : 2 − 100 = 307
964 : 4 • 3 − 810 : 3 = 453
295. Сравни уравнения каждой пары и их решения:
x + 75 = 125 • 3 x − 75 = 125 • 3
x = 375 − 75 x = 375 + 75
x = 300 x = 450
В первом уравнении действие сложение, а во втором − вычитание;
в первом уравнении неизвестное − первое слагаемое, а во втором − уменьшаемое;
первое уравнение решается вычитанием, а второе − сложением;
в обоих уравнениях встречается число 75, в первом случае это второе слагаемое, а во втором − вычитаемое;
уравнения объединяет то, что в обоих случаях в результате получается число, равное произведению чисел 125 и 3;
300 < 450
x • 10 = 250 x : 10 = 250
x = 250 : 10 x = 250 • 10
x = 25 x = 2 500
в первом уравнении действие умножение, а во втором − деление;
в первом уравнении неизвестное − первый множитель, а во втором − делимое;
первое уравнение решается действием делением, а второе − умножением;
в обоих уравнениях встречается число 10, в первом случае это второй множитель, а во втором − делитель;
уравнения объединяет то, что в обоих случаях и результате получается одно и то же число − 250;
25 < 2500
x : 7 = 140 140 : x = 7
x = 140 • 7 x = 140 : 7
x = 980 x = 20
в обоих уравнениях одно действие − деление;
в первом уравнении неизвестное делимое, а во втором − делитель;
первое уравнение решается умножением, а второе − делением;
в обоих уравнениях встречается число 7, в первом случае это делитель, а во втором − частное;
в обоих уравнениях встречается число 7, в первом случае это делитель, а во втором − частное;
в обоих уравнениях встречается число 140, в первом случае это частное, а во втором − делимое;
980 > 20
32 : x = 32 32 • x = 32
x = 32 : 32 x = 32 : 32
x = 1 x = 1
в первом уравнении действие деление, а во втором − умножение;
в первом уравнении неизвестное делитель, а во втором − второй множитель;
оба уравнения решатся делением;
в обоих уравнениях встречается число 32, в первом случае это делимое и частное, а во втором − первый множитель и произведение;
уравнения объединяет то, что в обоих случаях в результате получается одно и то же число − 32;
1 = 1
На сколько равных частей разделен каждый квадрат на чертеже? Найди площадь одной доли в каждом квадрате. Сравни площади этих долей.
Каждый квадрат разделён на 4 равные части.
2 • 2 = 4 (см2) − площадь каждого квадрата;
4 : 4 = 1 (см2) − площадь одной доли квадратов.
ЗАДАНИЕ НА ПОЛЯХ:
Ребус:
— 423 |9
36 |47
— 63
63
0
| ← Предыдущая | Следующая → |