Измерение величин
Прямоугольный параллелепипед
Ответы к стр. 112
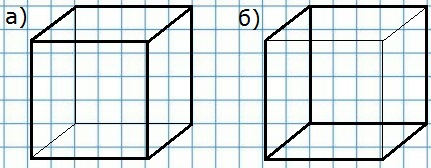
505. Перерисуйте рисунок 108 в тетрадь и обведите жирной линией видимые рёбра куба так, чтобы куб был виден:
а) сверху и справа; б) снизу и слева.

506. Рёбра прямоугольного параллелепипеда равны 3 см, 4 см и 5 см.
а) Найдите площадь его основания и площадь боковой поверхности, то есть сумму площадей боковых граней.
б) Найдите площадь полной поверхности прямоугольного параллелепипеда.
Объясните, почему в задании «а» могут получиться три разных ответа.
а) Три разных ответа возможны из-за разной длины трёх рёбер — получается шесть способов построения прямоугольного параллелепипеда, но из этих шести прямоугольных параллелепипедов у каждых двух будут одинаковы площади основания и боковой поверхности.
I вариант: длина — 5 см, ширина — 4 см, высота — 3 см (такие же площади будут при длине 4 см, ширине 5 см, высоте 3 см).
1) 5 • 4 = 20 (см2) − площадь основания
2) 3 • 4 = 12 (см2) − площадь первой грани
3) 3 • 5 = 15 (см2) − площадь второй грани
4) (12 + 15) • 2 = 54 (см2) − площадь боковой поверхности
О т в е т: 20 см2 − площадь основания, 54 см2 − площадь боковой поверхности.
II вариант: длина — 4 см, ширина — 3 см, высота — 5 см (такие же площади будут при длине 3 см, ширине 4 см, высоте 5 см).
1) 4 • 3 = 12 (см2) − площадь основания
2) 5 • 4 = 20 (см2) − площадь первой грани
3) 5 • 3 = 15 (см2) − площадь второй грани
4) (20 + 15) • 2 = 70 (см2) − площадь боковой поверхности
О т в е т: 12 см2 − площадь основания, 70 см2 − площадь боковой поверхности.
III вариант: длина — 3 см, ширина — 5 см, высота — 4 см (такие же площади будут при длине 5 см, ширине 3 см, высоте 4 см).
1) 3 • 5 = 15 (см2) − площадь основания
2) 4 • 3 = 12 (см2) − площадь первой грани
3) 4 • 5 = 20 (см2) − площадь второй грани
4) (12 + 20) • 2 = 64 (см2) − площадь боковой поверхности
О т в е т: 15 см2 − площадь основания, 64 см2 − площадь боковой поверхности.
б) I вариант: 20 • 2 + 54 = 94 (см2) − площадь полной поверхности
II вариант: 12 • 2 + 70 = 94 (см2) − площадь полной поверхности
III вариант: 15 • 2 + 64 = 94 (см2) − площадь полной поверхности
О т в е т: площадь полной поверхности во всех случаях 94 см2.
507. На рисунке 109 изображен куб, сложенный из восьми одинаковых кубиков с ребром 1 см. Сколько прямоугольных параллелепипедов на этом рисунке?
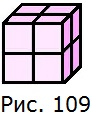
На рисунке один прямоугольный параллелепипед (куб), состоящий из:
а) 8 прямоугольных параллелепипедов (малых кубов) со сторонами 1 см;
б) 12 прямоугольных параллелепипедов со сторонами 1 см, 1 см и 2 см (состоят из 2 малых кубов);
в) 6 прямоугольных параллелепипедов со сторонами 2 см, 2 см и 1 см.
Итого: 1 + 8 + 12 + 6 = 27 прямоугольных параллелепипедов всего.
О т в е т: всего 27 прямоугольных параллелепипедов.
508. Окрашенный куб распилили на 27 одинаковых кубиков с ребром 1 см (рис. 110). У скольких маленьких кубиков окрашена только одна грань; только две грани; три грани?
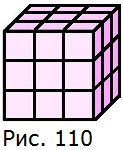
1 грань − у 6 маленьких кубиков (в центре каждой грани большого куба);
2 грани − у 12 кубиков (в середине с краю каждого ребра большого куба);
3 грани − у 8 кубиков (в каждой вершине большого куба).
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.