Делимость натуральных чисел
Делители натурального числа
Ответы к стр. 145
646. а) Что называют делителем натурального числа; простым делителем натурального числа?
б) Что значит разложить число на простые множители?
а) Если натуральное число α делится на натуральное число b, то число b называют делителем числа α. Если делитель — простое число, его называют простым делителем.
б) Разложить данное составное число на простые множители — значит представить его в виде произведения различных его простых делителей или их степеней.
647. Укажите все делители числа:
а) 2; б) 6; в) 12; г) 16; д) 18; е) 20;
ж) 1; з) 48; и) 100; к) 104; л) 121; м) 256.
а) 2¦2
1¦
Делители 1, 2.
б) 6¦2
3¦3
1¦
Делители 1, 2, 3, 6.
в) 12¦2
6¦2
3¦3
1¦
Делители 1, 2, 3, 4, 6, 12.
г) 16¦2
8¦2
4¦2
2¦2
1¦
Делители 1, 2, 4, 8, 16.
д) 18¦2
9¦3
3¦3
1¦
Делители 1, 2, 3, 6, 9, 18.
е) 20¦2
10¦2
5¦5
1¦
Делители 1, 2, 4, 5, 10, 20.
ж) 1¦1
1¦
Делитель 1.
з) 48¦2
24¦2
12¦2
6¦2
3¦3
1¦
Делители 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
и) 100¦2
50¦2
25¦5
5¦5
1¦
Делители 1, 2, 4, 5, 10, 20, 25, 50, 100.
к) 104¦2
52¦2
26¦2
13¦13
1¦
Делители 1, 2, 4, 8, 13, 26, 52, 104.
л) 121¦11
11¦11
1¦
Делители 1, 11, 121.
м) 256¦2
128¦2
64¦2
32¦2
16¦2
8¦2
4¦2
2¦2
1¦
Делители 1, 2, 4, 8, 16, 32, 64, 128, 256.
648. Запишите пять натуральных чисел, имеющих делителями числа:
а) 2; б) 3; в) 4; г) 5; д) 9;
е) 10; ж) 2 и 3; з) 3 и 4; и) 2 и 5; к) 4 и 9.
а) 2 = 1 • 2
4 = 2 • 2
6 = 3 • 2
8 = 4 • 2
10 = 5 • 2
О т в е т: 2, 4, 6, 8, 10.
б) 3 = 1 • 3
6 = 2 • 3
9 = 3 • 3
12 = 4 • 3
15 = 5 • 3
О т в е т: 3, 6, 9, 12, 15.
в) 4 = 1 • 4
8 = 2 • 4
12 = 3 • 4
16 = 4 • 4
20 = 5 • 4
О т в е т: 4, 8, 12, 16, 20.
г) 5 = 1 • 5
10 = 2 • 5
15 = 3 • 5
20 = 4 • 5
25 = 5 • 5
О т в е т: 5, 10, 15, 20, 25.
д) 9 = 1 • 9
18 = 2 • 9
27 = 3 • 9
36 = 4 • 9
45 = 5 • 9
О т в е т: 9, 18, 27, 36, 45.
е) 10 = 1 • 10
20 = 2 • 10
30 = 3 • 10
10 = 4 • 10
50 = 5 • 10
О т в е т: 10, 20, 30, 40, 50.
ж) 6 = 1 • (2 • 3) = 1 • 6
12 = 2 • (2 • 3) = 2 • 6
18 = 3 • (2 • 3) = 3 • 6
24 = 4 • (2 • 3) = 4 • 6
30 = 5 • (2 • 3) = 5 • 6
О т в е т: 6, 12, 18, 24, 30.
з) 12 = 1 • (3 • 4) = 1 • 12
24 = 2 • (3 • 4) = 2 • 12
36 = 3 • (3 • 4) = 3 • 12
48 = 4 • (3 • 4) = 4 • 12
60 = 5 • (3 • 4) = 5 • 12
О т в е т: 12, 24, 36, 48, 60.
и) 10 = 1 • (2 • 5) = 1 • 10
20 = 2 • (2 • 5) = 2 • 10
30 = 3 • (2 • 5) = 3 • 10
10 = 4 • (2 • 5) = 4 • 10
50 = 5 • (2 • 5) = 5 • 10
О т в е т: 10, 20, 30, 40, 50.
к) 36 = 1 • (4 • 9) = 1 • 36
72 = 2 • (4 • 9) = 2 • 36
108 = 3 • (4 • 9) = 3 • 36
144 = 4 • (4 • 9) = 4 • 36
180 = 5 • (4 • 9) = 5 • 36
О т в е т: 36, 72, 108, 144, 180.
649. Запишите пять натуральных чисел, не имеющих других простых делителей, кроме: а) 2; б) 3; в) 5; г) 2 и 3; д) 2 и 5.
а) 2 = 21
4 = 22
8 = 23
16 = 24
32 = 25
О т в е т: 2, 4, 8, 16, 32.
б) 3 = 31
9 = 32
27 = 33
81 = 34
243 = 35
О т в е т: 3, 9, 27, 81, 243.
в) 5 = 51
25 = 52
125 = 53
625 = 54
3125 = 55
О т в е т: 5, 25, 125, 625, 3125.
г) 6 = 2 • 3
12 = 22 • 3 = 4 • 3
18 = 2 • 32 = 2 • 9
24 = 23 • 3 = 8 • 3
36 = 22 • 32 = 4 • 9
О т в е т: 6, 12, 18, 24, 36.
д) 10 = 2 • 5
20 = 22 • 5 = 4 • 5
40 = 23 • 5 = 8 • 5
50 = 2 • 52 = 2 • 25
100 = 22 • 52 = 4 • 25
О т в е т: 10, 20, 40, 50, 100.
650. Найдите все делители числа α:
а) α = 2 • 3 • 5; б) α = 3 • 5 • 7; в) α = 3 • 3 • 11; г) α = 3 • 5 • 5 • 7.
Решение. а) Число α имеет простые делители: 2, 3 и 5. Другие делители найдем, составляя различные произведения из этих простых делителей: 2 • 3 = 6; 2 • 5 = 10; 3 • 5 = 15; 2 • 3 • 5 = 30. Кроме того, число α делится на 1.
Ответ: 1, 2, 3, 5, 6, 10, 15, 30.
б) Число α имеет простые делители: 3, 5 и 7. Другие делители найдем, составляя различные произведения из этих простых делителей: 3 • 5 = 15; 3 • 7 = 21; 5 • 7 = 35; 3 • 5 • 7 = 105. Кроме того, число α делится на 1.
О т в е т: 1, 3, 5, 7, 15, 21, 35, 105.
в) Число α имеет простые делители: 3, 3 и 11. Другие делители найдем, составляя различные произведения из этих простых делителей: 3 • 3 = 9; 3 • 11 = 33; 3 • 3 • 11 = 99. Кроме того, число α делится на 1.
О т в е т: 1, 3, 9, 11, 33, 99.
г) Число α имеет простые делители: 3, 5, 5 и 7. Другие делители найдем, составляя различные произведения из этих простых делителей: 3 • 3 = 15; 3 • 7 = 21; 5 • 5 = 25; 5 • 7 = 35; 3 • 5 • 5 = 75; 3 • 5 • 7 = 105; 5 • 5 • 7 = 175; 3 • 5 • 5 • 7 = 525. Кроме того, число α делится на 1.
О т в е т: 1, 3, 5, 7, 15, 21, 25, 35, 75, 105, 175, 525.
651. Разложите на простые множители число:
а) 16; б) 18; в) 26; г) 35; д) 48; е) 70;
ж) 144; з) 210; и) 800; к) 216; л) 343; м) 1024.
а) 16¦2
8¦2
4¦2
2¦2
1¦
16 = 24
б) 18¦2
9¦3
3¦3
1¦
18 = 2 • 32
в) 26¦2
13¦13
1¦
26 = 2 • 13
г) 35¦5
7¦7
1¦
35 = 5 • 7
д) 48¦2
24¦2
12¦2
6¦2
3¦3
1¦
48 = 24 • 3
е) 70¦2
35¦5
7¦7
1¦
70 = 2 • 5 • 7
ж) 144¦2
72¦2
36¦2
18¦2
9¦3
3¦3
1¦
144 = 24 • 32
з) 210¦2
105¦3
35¦5
7¦7
1¦
210 = 2 • 3 • 5 • 7
и) 800¦2
400¦2
200¦2
100¦2
50¦2
25¦5
5¦5
1¦
800 = 25 • 52
к) 216¦2
108¦2
54¦2
27¦3
9¦3
3¦3
1¦
216 = 23 • 33
л) 343¦7
49¦7
7¦7
1¦
343 = 73
м) 1024¦2
512¦2
256¦2
128¦2
64¦2
32¦2
16¦2
8¦2
4¦2
2¦2
1¦
1024 = 210
652. Представьте данное произведение в виде произведения возможно большего числа множителей, отличных от 1:
а) 20 • 24; б) 12 • 25; в) 164 • 10; г) 8 • 125;
д) 125 • 64; е) 112 • 147; ж) 1001 • 37; з) 47 • 201.
а) 20¦2 24¦2
10¦2 12¦2
5¦5 6¦2
1¦ 3¦3
1¦
20 • 24 = 25 • 5 • 3 = 480
б) 12¦2 25¦5
6¦2 5¦5
3¦3 1¦
1¦
12 • 25 = 22 • 52 • 3 = 300
в) 164¦2 10¦2
82¦2 5¦5
41¦41 1¦
1¦
164 • 10 = 23 • 5 • 41 = 1640
г) 8¦2 125¦5
4¦2 25¦5
2¦2 5¦5
1¦ 1¦
8 • 125 = 23 • 53 = 1000
д) 125¦5 64¦2
25¦5 32¦2
5¦5 16¦2
1¦ 8¦2
4¦2
2¦2
1¦
125 • 64 = 53 • 26 = 8000
е) 112¦2 147¦3
56¦2 49¦7
28¦2 7¦7
14¦2 1¦
7¦7
1¦
112 • 147 = 24 • 3 • 73 = 16 464
ж) 1001¦7 37¦37
143¦11 1¦
13¦13
1¦
1001 • 37 = 7 • 11 • 13 • 37 = 37 037
з) 47¦47 201¦3
1¦ 67¦67
1¦
47 • 201 = 3 • 47 • 67 = 9447
653. Запишите в порядке возрастания все делители числа:
а) 12; б) 15; в) 18; г) 24.
а) 12¦2
6¦2
3¦3
1¦
Делители: 1, 2, 3, 4 (2 • 2), 6 (2 • 3), 12 (2 • 2 • 3).
б) 15¦3
5¦5
1¦
Делители: 1, 3, 5, 15 (3 • 5).
в) 18¦2
9¦3
3¦3
1¦
Делители: 1, 2, 3, 6 (2 • 3), 9 (3 • 3), 18 (2 • 3 • 3).
г) 24¦2
12¦2
6¦2
3¦3
1¦
Делители: 1, 2, 3, 4 (2 • 2), 6 (2 • 3), 8 (2 • 2 • 2), 12 (2 • 2 • 3), 24 (2 • 2 • 2 • 3).
654. Выполняя предыдущее задание, можно заметить, что делители числа 18 обладают интересным свойством:
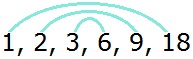
1 • 18 = 2 • 9 = 3 • 6 = 18
Это наблюдение позволяет сократить перебор чисел при поиске всех делителей числа 18. Сначала перебираем все делители числа 18 до тех пор, пока произведение двух соседних делителей не даст 18: 1, 2, 3, 6. После того как найдена «середина» в ряду делителей, остальные делители найдем делением: 18 : 2 = 9, 18 : 1 = 18. Используя этот прием, найдите все делители числа: а) 32; б) 48; в) 56; г) 36; д) 98.
а) Перебираем все делители числа 32 до тех пор, пока произведение двух соседних делителей не даст 32: 1, 2, 4, 8. После того, как найдена «середина» в ряду делителей, остальные делители найдем делением: 32 : 2 = 16, 32 : 1 = 32. Делители числа 32: 1, 2, 4, 8, 16, 32.
б) Перебираем все делители числа 48 до тех пор, пока произведение двух соседних делителей не даст 48: 1, 2, 3, 4, 6, 8. После того, как найдена «середина» в ряду делителей, остальные делители найдем делением: 48 : 4 = 12, 48 : 3 = 16, 48 : 2 = 24, 48 : 1 = 48. Делители числа 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
в) Перебираем все делители числа 56 до тех пор, пока произведение двух соседних делителей не даст 56: 1, 2, 4, 7, 8. После того, как найдена «середина» в ряду делителей, остальные делители найдем делением: 56 : 4 = 14, 56 : 2 = 28, 56 : 1 = 56. Делители числа 56: 1, 2, 4, 7, 8, 14, 28, 56.
г) Перебираем все делители числа 36 до тех пор, пока произведение двух соседних делителей не даст 36: 1, 2, 3, 4, 6. После того, как найдена «середина» в ряду делителей, остальные делители найдем делением: 36 : 4 = 9, 36 : 3 = 12, 36 : 2 = 18, 36 : 1 = 36. Делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
д) Перебираем все делители числа 98 до тех пор, пока произведение двух соседних делителей не даст 98: 1, 2, 7, 14. После того, как найдена «середина» в ряду делителей, остальные делители найдем делением: 98 : 2 = 49, 98 : 1 = 98. Делители числа 98: 1, 2, 7, 14, 49, 98.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.