Делимость натуральных чисел
Занимательные задачи
Ответы к стр. 162
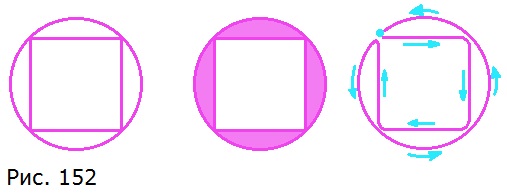
724. Нарисуйте по правилам, приведенным в задаче 723, фигуру, изображенную на рисунке 152.
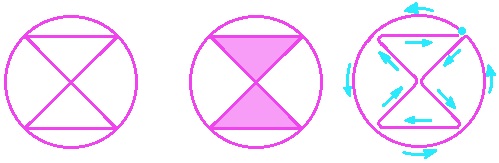
725. Нарисуйте по тем же правилам (см. задачу 723) фигуру, изображенную на рисунке 153.
726. Придумайте свои фигуры, которые можно нарисовать, не отрывая карандаша от бумаги, не проводя по линии дважды и без самопересечений.
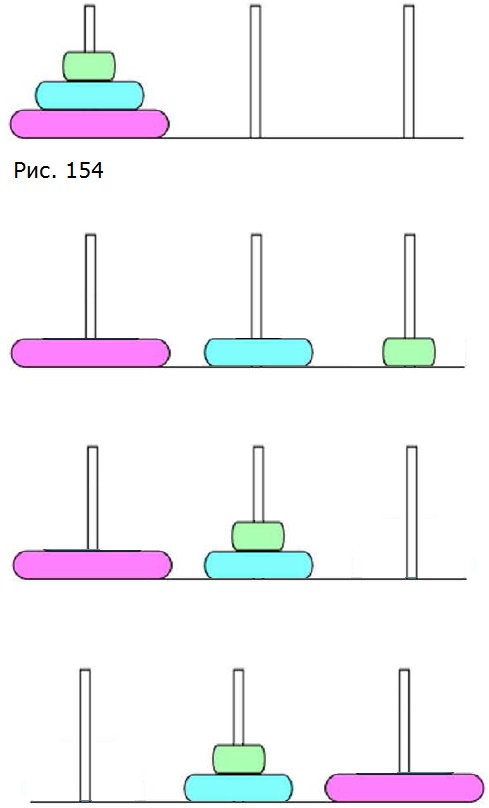
727. Головоломка. Имеется 3 штырька, на один из которых насажены 3 кольца (рис. 154). За сколько ходов можно перенести пирамиду из этих трёх колец на другой штырёк, если за один ход разрешается переносить только одно кольцо; при этом нельзя большее кольцо класть на меньшее.
Решите задачу: а) для четырёх колец; б) для пяти колец.
Сначала решим задачу для двух колец. Очевидно, что пирамиду из двух колец можно перенести за три хода.
Чтобы перенести пирамиду из трёх колец, сначала перенесем на свободный штырёк пирамиду из двух колец. Для этого требуется 3 хода. Перенесем нижнее кольцо на свободный штырёк. Наконец, опять за три хода перенесем пирамиду из двух колец на тот штырёк, где уже находится большее кольцо. Пирамиду из трёх колец можно перенести за: 3 + 1 + 3 = 7 ходов.
Тогда:
а) 7 + 1 + 7 = 15 (ходов) — нужно, чтобы перенести пирамиду из четырёх колец;
б) 15 + 1 + 15 = 31 (ход) — нужно, чтобы перенести пирамиду из пяти колец.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.