Натуральные числа и нуль
Исторические сведения
Ответы к стр. 69
301. Первый магический квадрат был составлен в Китае в V−IV веке до н.э. Другой магический квадрат был составлен в Индии в I веке н.э. Сравните суммы чисел в строчках, столбцах и диагоналях квадратов. В чём заключается магическое свойство этих квадратов?
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
| 1 | 14 | 15 | 4 |
| 12 | 7 | 6 | 9 |
| 8 | 11 | 10 | 5 |
| 13 | 2 | 3 | 16 |
Суммы чисел в строках, столбцах и диагоналях равны.
302. В квадрате 3×3 расставьте числа 0, 1, 2, 3, 4, 5, 6, 7, 8 так, чтобы сумма чисел в каждой строке, в каждом столбце и на каждой диагонали была одинакова. Сначала определите, какой должна быть эта сумма.
0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36, 36 : 3 = 12 — это сумма трёх чисел. Если разбить числа по парам с начала и конца ряда (0 + 8, 1 + 7, 2 + 6, 3 + 5), то останется число 4. При этом сумма пар всегда равна 8, а 8 + 4 = 12 — искомая сумма чисел в магическом квадрате. Следовательно, число 4 будет стоять в центре квадрата.
| 1 | 8 | 3 |
| 6 | 4 | 2 |
| 5 | 0 | 7 |
303. Докажите, что сумма всех чисел любого магического квадрата 3×3 делится на 3.
Суммы в каждой строке магического квадрата равны между собой. Всего строк три и сумму всех чисел квадрата можно представить как сумму чисел одной строки умноженной на 3. Если это произведение разделить на 3, то получится сумма чисел одной строки, следовательно, сумма всех чисел делится на 3.
304. В Древней Индии умножали многозначные числа совсем не так, как мы это делаем теперь. Чтобы перемножить, например, 537 и 82, индусы рисовали прямоугольник со сторонами 3 и 2 клетки (по числу цифр в записи множителей), подписывали рядом с клетками прямоугольника цифры первого числа слева направо, цифры второго числа снизу вверх, клетки прямоугольника делили диагоналями (рис. 28). Затем перемножали попарно цифры множителей и результат записывали в соответствующую клетку таблицы так: цифру единиц писали вверху клетки, цифру десятков − внизу. После этого складывали полученные результаты вдоль диагоналей квадратов. Считать начинали с правого верхнего угла квадрата. Так получали цифры ответа по разрядам. В нашем примере:
единицы: 4
десятки : 6 + 1 + 6 = 13 (3 пишем, 1 запоминаем) 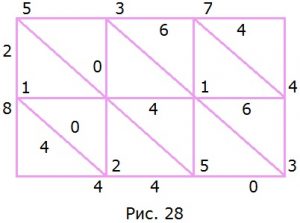
сотни: 0 + 4 + 5 + 1 = 10 (0 пишем, 1 запоминаем)
тысячи: 1 + 0 + 2 + 1 = 4
десятки тысяч: 4
Ответ: 537 • 82 = 44034.
Проверим результаты обычным способом:
×537
82
+ 1074
4296
44034
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.