Обыкновенные и десятичные дроби
Задачи на составление и разрезание фигур
Ответы к стр. 225
1079. У шахматной доски отрезали две противоположные угловые клетки (рис. 143). Можно ли эту доску разрезать на фигуры домино, покрывающие две клетки доски?
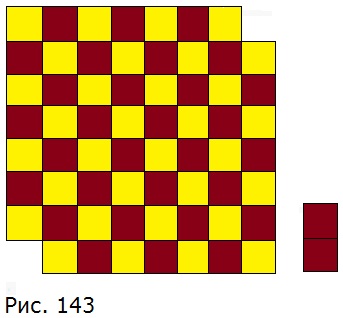
Видимо на рисунке в учебнике ошибка — обрезанные клетки не могут быть жёлтого цвета, они коричневые.
После обрезания доски на ней осталось 32 жёлтых и 30 коричневых клеток. Фигуры домино будут состоять из двух цветов: одной клетки коричневого цвета и одной клетки жёлтого цвета, так как на доске соседние клетки имеют разные цвета. Тогда каждая фигура домино будет убавлять от доски одинаковое количество коричневых и жёлтых клеток, а поскольку коричневых клеток на 2 меньше, чем жёлтых и соседние клетки не могут быть одинакового цвета, разрезать доску на фигуры домино невозможно.
1080. Прямоугольник 2 × 4 состоит из 8 квадратов. Разрежьте прямоугольник на две равные части так, чтобы линия разреза шла по сторонам квадратов. Найдите три способа разрезания.
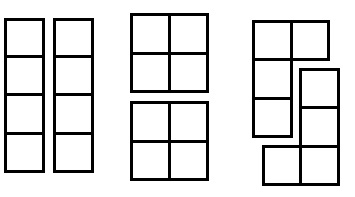
1081. Квадрат 4 × 4 состоит из 16 квадратов. Разрежьте его на: а) две; б) четыре равные части так, чтобы линия разреза шла по сторонам квадратов. Сколько способов разрезания вы найдёте?
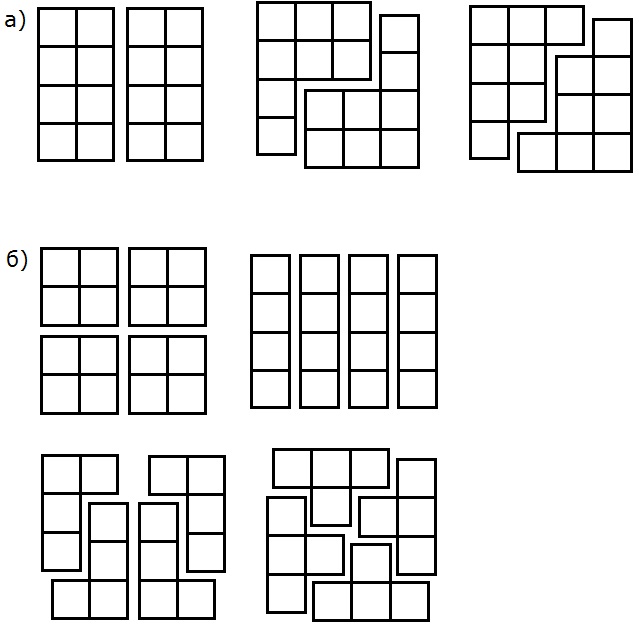
1082. Прямоугольник 4 × 6 состоит из 24 квадратов. Разрежьте его на шесть равных частей так, чтобы линия разреза шла по сторонам квадратов.
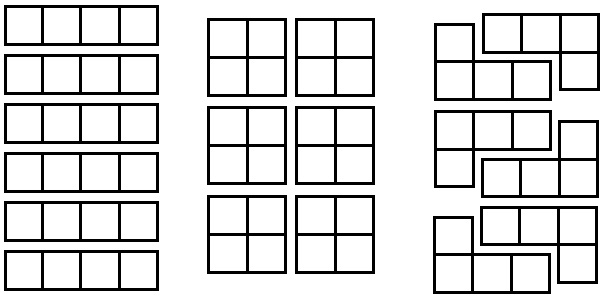
1083. Разрежьте фигуру, состоящую из квадратов (рис. 144), на три равные части так, чтобы линия разреза шла по сторонам квадратов.
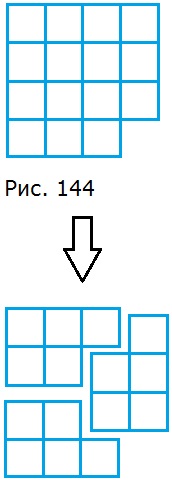
1084. Разрежьте фигуру, состоящую из квадратов (рис. 145), на четыре равные части так, чтобы линия разреза шла по сторонам квадратов.
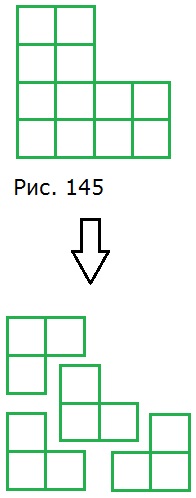
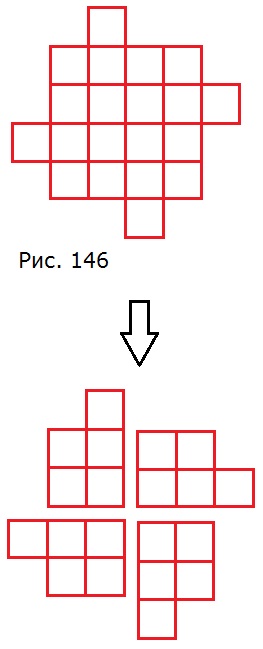
1085. Разрежьте фигуру, состоящую из квадратов (рис. 146), на четыре равные части так, чтобы линия разреза шла по сторонам квадратов.
| ← Предыдущая | Следующая → |
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.