Отношения, пропорции, проценты
Вероятность события
Ответы к стр. 40
172. Бросают игральный кубик. Какова вероятность того, что выпадет число очков:
а) делящееся и на 2, и на 3;
б) делящееся на 2 и не делящееся на 3;
в) делящееся на 3 и не делящееся на 2;
г) не делящееся ни на 2, ни на 3;
д) делящееся или на 2, или на 3?
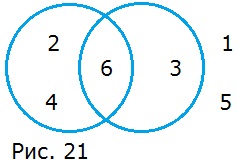
У к а з а н и е. Решите задачу, используя рисунок 21.
На рисунке в первом круге числа 2, 4 и 6 делятся на 2. Во втором круге числа 6 и 3 делятся на 3. Число 6 в пересечении кругов делится и на 2, и на 3. Числа 2 и 4 в первом круге делятся только на 2. Числа 1 и 5 за кругом не делятся ни на 2, ни на 3.
Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так на кубике 6 граней.
а) Количество случаев, благоприятствующих выпадению числа делящегося и на 2 и на 3 равно 1, так как такое число только одно — 6. Вероятность события равна 1/6.
б) Количество случаев, благоприятствующих выпадению числа, делящегося на 2 и не делящегося на 3 равно 2, так как таких чисел два: 2 и 4. Вероятность события равна 2/6 = 1/3.
в) Количество случаев, благоприятствующих выпадению числа, делящегося на 3 и не делящееся на 2 равно 1, так как такое число только одно — 3. Вероятность события равна 1/6.
г) Количество случаев, благоприятствующих выпадению числа, не делящееся ни на 2, ни на 3 равно 2, так как таких чисел два: 1 и 5. Вероятность события равна 2/6 = 1/3.
д) Количество случаев, благоприятствующих выпадению числа, делящегося или на 2, или на 3 равно 4, так как таких чисел четыре: 2, 3, 4 и 6. Вероятность события равна 4/6 = 2/3.
173. Бросают два игральных кубика. Какова вероятность события:
а) A: «сумма очков равна 2»;
б) B: «сумма очков равна 10»;
в) C: «сумма очков равна 12»;
г) D: «сумма очков равна 13»;
д) E: «сумма очков равна 1»;
е) F: «сумма очков равна одному из натуральных чисел 2, 3, …, 11, 12»?
Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так как на кубике 6 граней. Так как кубика два, то число всех равновозможных случаев, одно из которых обязательно произойдет, будет 6 • 6 = 36.
а) Чтобы сумма очков была 2, может быть 1 вариант: 1 + 1. Тогда вероятность события равна 1/36.
б) Чтобы сумма очков была 10, могут быть 3 варианта: 4 + 6, 5 + 5 и 6 + 4. Тогда вероятность события равна 3/36 = 1/12.
в) Чтобы сумма очков была 12, может быть 1 вариант: 6 + 6. Тогда вероятность события равна 1/36.
г) Максимальная сумма очков на двух кубиках равна 12, поэтому сумма 13 очков получиться не может, следовательно, количество случаев, благоприятствующих выпадению суммы в 13 очков, равно 0. Тогда вероятность события равна 0/36 = 0.
д) Минимальная сумма очков на двух кубиках равна 2, поэтому сумма 1 очко получится не может, следовательно, количество случаев, благоприятствующих выпадению суммы в 1 очко, равно 0. Тогда вероятность события равна 0/36 = 0.
е) При сложении чисел на двух гранях кубика всегда получится сумма очков, равная одному из натуральных чисел 2, 3, …, 11, 12, поэтому количество случаев, благоприятствующих выпадению данной суммы равно 36. Тогда вероятность события равна 36/36 = 1.
174. В первом ряду микроавтобуса имеется только 3 места. На них собираются сесть двое мужчин и одна женщина. Какова вероятность того, что мужчины окажутся рядом?
Число всех равновозможных случаев, одно из которых обязательно произойдет при рассадке пассажиров равно 3: мужчина-мужчина-женщина, мужчина-женщина-мужчина, женщина-мужчина-мужчина. Так как для того, чтобы мужчины оказались рядом, женщина обязательно должна сидеть на крайнем сидении, то количество благоприятствующих для этого случаев равно 2. Тогда вероятность того, что мужчины окажутся рядом равна 2/3.
175. Бросают две монеты. Если выпадут два орла, то выиграл 1-й, если выпадут орёл и решка, то выиграл 2-й. Справедлива ли эта игра?
В результате подбрасывания двух монет возможно 4 исхода:
1) орёл, орёл;
2) орёл, решка;
3) решка, орёл;
4) решка, решка.
Из них в одном случае (1) выпадает два орла. Следовательно, вероятность события равна 1/4.
В двух случаях (2 и 3) выпадает орёл и решка. Следовательно, вероятность события равна 2/4.
1/4 < 2/4, то есть игра не справедлива (больше шансов выиграть у второго игрока).
176. Бросают два игральных кубика. Если сумма очков 11 − выиграл 1-й, если сумм очков 12 − выиграл 2-й. Справедлива ли эта игра?
Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так как на кубике 6 граней. Так как кубика два, то число всех равновозможных случаев, одно из которых обязательно произойдет, будет 6 • 6 = 36.
Чтобы сумма очков была 11, могут быть 2 варианта: 5 + 6 и 6 + 5. Тогда вероятность события равна 2/36.
Чтобы сумма очков была 12, может быть 1 вариант: 6 + 6. Тогда вероятность события равна 1/36.
2/36 > 1/36, то есть игра не справедлива (больше шансов выиграть у первого игрока).
Придумываем задачу
177. Придумайте справедливую и несправедливую игру:
а) с двумя игральными кубиками; б) с двумя монетами.
а) Справедливая. Бросают два игральных кубика. Если сумма очков 2 − выиграл 1-й, если сумм очков 12 − выиграл 2-й.
Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так как на кубике 6 граней. Так как кубика два, то число всех равновозможных случаев, одно из которых обязательно произойдет, будет 6 • 6 = 36.
Чтобы сумма очков была 2, может быть 1 вариант: 1 + 1. Тогда вероятность события равна 1/36.
Чтобы сумма очков была 12, может быть 1 вариант: 6 + 6. Тогда вероятность события равна 1/36.
1/36 = 1/36, то есть игра справедлива.
а) Несправедливая. Бросают два игральных кубика. Если сумма очков 10 − выиграл 1-й, если сумм очков 12 − выиграл 2-й.
Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так как на кубике 6 граней. Так как кубика два, то число всех равновозможных случаев, одно из которых обязательно произойдет, будет 6 • 6 = 36.
Чтобы сумма очков была 10, могут быть 3 варианта: 4 + 6, 5 + 5 и 6 + 4. Тогда вероятность события равна 3/36.
Чтобы сумма очков была 12, может быть 1 вариант: 6 + 6. Тогда вероятность события равна 1/36.
3/36 > 1/36, то есть игра не справедлива (больше шансов выиграть у первого игрока).
б) Справедливая. Бросают две монеты. Если выпадут два орла, то выиграл 1-й, если выпадут две решки, то выиграл 2-й.
В результате подбрасывания двух монет возможно 4 исхода:
1) орёл, орёл;
2) орёл, решка;
3) решка, орёл;
4) решка, решка.
Из них в одном случае (1) выпадает два орла. Следовательно, вероятность события равна 1/4.
В одном случае (4) выпадает две решки. Следовательно, вероятность события равна 1/4.
1/4 = 1/4, то есть игра справедлива.
б) Несправедливая. Бросают две монеты. Если выпадут два орла, то выиграл 1-й, если выпадет хотя бы одна решка, то выиграл 2-й.
В результате подбрасывания двух монет возможно 4 исхода:
1) орёл, орёл;
2) орёл, решка;
3) решка, орёл;
4) решка, решка.
Из них в одном случае (1) выпадает два орла. Следовательно, вероятность события равна 1/4.
В трёх случаях (2, 3 и 4) выпадает хотя бы одна решка. Следовательно, вероятность события равна 3/4.
1/4 < 3/4, то есть игра не справедлива (больше шансов выиграть у второго игрока).
178. Витя задумал число, записанное цифрами 1, 2, 3, 4, 5 без повторения. Коля пытается это число угадать. Какова вероятность того что Коля угадает число с первого раза, если это число:
а) двузначное; б) трёхзначное; в) четырёхзначное?
а) На первом месте числа может оказаться одна из пяти цифр. На втором месте может оказаться одна из четырёх оставшихся цифр. Тогда общее количество полученных сочетаний цифр будет 5 • 4 = 20 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 20, так как 20 двузначных чисел можно составить из цифр 1, 2, 3, 4, 5 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Коля должен с первого раза. Тогда вероятность того, что Коля угадает двузначное число с первого раза равна 1/20.
б) На первом месте числа может оказаться одна из пяти цифр. На втором месте может оказаться одна из четырёх оставшихся цифр, а на третьем — одна из трёх оставшихся. Тогда общее количество полученных сочетаний цифр будет 5 • 4 • 3 = 60 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 60, так как 60 трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Коля должен с первого раза. Тогда вероятность того, что Коля угадает трёхзначное число с первого раза равна 1/60.
в) На первом месте числа может оказаться одна из пяти цифр. На втором месте может оказаться одна из четырёх оставшихся цифр. На третьем месте может оказаться одна из трёх оставшихся цифр, а на четвёртом — одна из двух оставшихся. Тогда общее количество полученных сочетаний цифр будет 5 • 4 • 3 • 2 = 120 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 120, так как 120 четырёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Коля должен с первого раза. Тогда вероятность того, что Коля угадает четырёхзначное число с первого раза равна 1/120.
179. Коля задумал число, записанное цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9 без повторения. Витя пытается это число угадать. Какова вероятность того, что Витя угадает число с первого раза, если это число:
а) двузначное; б) трёхзначное; в) четырёхзначное?
а) На первом месте числа может оказаться одна из девяти цифр. На втором месте может оказаться одна из восьми оставшихся цифр. Тогда общее количество полученных сочетаний цифр будет 9 • 8 = 72 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 72, так как 72 двузначных числа можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Витя должен с первого раза. Тогда вероятность того, что Витя угадает двузначное число с первого раза равна 1/72.
б) На первом месте числа может оказаться одна из девяти цифр. На втором месте может оказаться одна из восьми оставшихся цифр, а на третьем — одна из семи оставшихся. Тогда общее количество полученных сочетаний цифр будет 9 • 8 • 7 = 504 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 504, так как 504 трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Витя должен с первого раза. Тогда вероятность того, что Витя угадает трёхзначное число с первого раза равна 1/504.
в) На первом месте числа может оказаться одна из девяти цифр. На втором месте может оказаться одна из восьми оставшихся цифр. На третьем месте может оказаться одна из семи оставшихся цифр, а на четвёртом — одна из шести оставшихся. Тогда общее количество полученных сочетаний цифр будет 9 • 8 • 7 • 6 = 3024 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 3024, так как 3024 четырёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Витя должен с первого раза. Тогда вероятность того, что Витя угадает четырёхзначное число с первого раза равна 1/3024.
| ← Предыдущая | Следующая → |
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.