Отношения, пропорции, проценты
Занимательные задачи
Ответы к стр. 44
Исследуем
195. Две фигуры называют равновеликими если их площади равны.
а) Постройте прямоугольник со сторонами 6 см и 4 см. Постройте два прямоугольника, равновеликие с построенным.
б) Какие стороны может иметь прямоугольник, равновеликий квадрату со стороной 8 см?
в) Какой наибольший периметр имеет прямоугольник, равновеликий квадрату со стороной 10 см?
Стороны прямоугольника выражаются натуральными числами.
а) 6 см • 4 см = 24 см2 — площадь прямоугольника
Стороны равновеликого ему прямоугольника могут иметь стороны:
24 см2 = 2 см и 12 см;
24 см2 = 3 см и 8 см.
б) Стороны квадрата равны, тогда: 8 см • 8 см = 64 см2 — площадь квадрата со стороной 8 см.
Стороны равновеликого ему прямоугольника могут иметь стороны:
64 см2 = 1 см и 64 см;
64 см2 = 2 см и 32 см;
64 см2 = 16 см и 4 см.
в) Стороны квадрата равны, тогда: 10 см • 10 см = 100 см2 — площадь квадрата со стороной 10 см.
Стороны равновеликого ему прямоугольника могут иметь стороны:
100 см2 = 1 см и 100 см;
100 см2 = 2 см и 50 см;
100 см2 = 4 см и 25 см.
Периметр прямоугольника равен сумме длин всех его сторон, тогда:
2 • (1 см + 100 см) = 202 см;
2 • (2 см + 50 см) = 104 см;
2 • (4 см + 25 см) = 58 см.
Периметр прямоугольника со сторонами 1 см и 100 см наибольший.
Доказываем
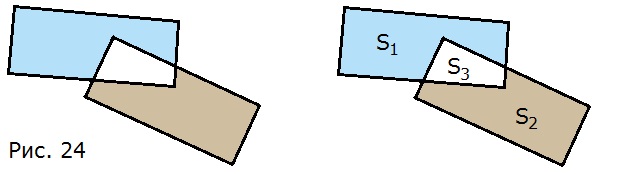
196. Две равные фигуры наложили друг на друга (рис. 24). Докажите, что площади закрашенных фигур равны.
Обозначим площадь голубой части как S1, площадь серой части как S2, площадь белой части как S3, тогда:
— площадь первого прямоугольника равна S1 + S3;
— площадь второго прямоугольника равна S2 + S3.
Так как по условию задачи прямоугольники равны, то:
S1 + S3 = S2 + S3
S1 = S2 + S3 — S3
S1 = S2 — то есть площади закрашенных фигур равны.
197. Вычислите площадь треугольника (рис. 25).
а) AD = 15 мм, DB = 20 мм.
Достраиваем треугольник ABD до прямоугольника ACBD.
Площадь прямоугольника равна: SACBD = AD • DB = 15 мм • 20 мм = 300 мм2.
Прямоугольник состоит из двух равных треугольников, тогда площадь треугольника ABD равна: 300 мм2 : 2 = 150 мм2.
б) DC = 20 мм, DB = 20 мм.
Достраиваем треугольник DBC до прямоугольника DBAC. Так как DC = DB, то получился квадрат со стороной 20 мм.
Площадь квадрата равна: SDBAC = DC • DB = 20 мм • 20 мм = 400 мм2.
Квадрат состоит из двух равных треугольников, тогда площадь треугольника BDC равна: 400 мм2 : 2 = 200 мм2.
в) AD = 15 мм, DB = 20 мм.
Достраиваем треугольник ABD до прямоугольника AEBD.
Площадь прямоугольника равна: SAEBD = AD • DB = 15 мм • 20 мм = 300 мм2.
Прямоугольник состоит из двух равных треугольников, тогда площадь треугольника ABD равна: 300 мм2 : 2 = 150 мм2.
DC = 20 мм, DB = 20 мм.
Достраиваем треугольник DBC до прямоугольника DBFC. Так как DC = DB, то получился квадрат со стороной 20 мм.
Площадь квадрата равна: SDBFC = DC • DB = 20 мм • 20 мм = 400 мм2.
Квадрат состоит из двух равных треугольников, тогда площадь треугольника BDC равна: 400 мм2 : 2 = 200 мм2.
Площадь фигуры равна сумме площадей составляющих её частей, следовательно, площадь треугольника ABC = площадь треугольника ABD + площадь треугольника BDC = 150 мм2 + 200 мм2 = 350 мм2.
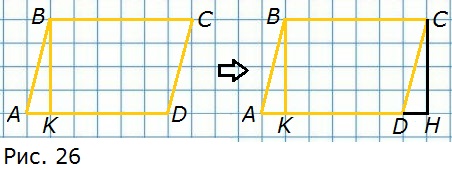
198. На рисунке 26 изображен параллелограмм (четырёхугольник, противоположные стороны которого попарно параллельны). Вычислите его площадь, если AD = 3 см, BK = 2 см.
Из точки C проведём отрезок CH параллельный и равный отрезку BK. Треугольники ABK и CDH равны, тогда прямоугольники ABCD и BCHK равновеликие, то есть их площади равны.
AD = BC = 3 см, BK = CH = 2 см.
Площадь BCHK = BC • CH = 3 см • 2 см = 6 см2.
Площадь ABCD = площадь BCHK = 6 см2.
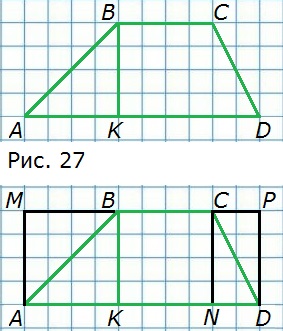
199. На рисунке 27 изображена трапеция (четырёхугольник, две стороны которого параллельны, а две другие — не параллельны). Вычислите её площадь, если AD = 5 см, BC = 2 см, BK = 2 см.
Достроим трапецию до прямоугольника AMPD.
BK = PD = 2 см.
Площадь прямоугольника AMPD = AD • PD = 5 см • 2 см = 10 см2.
Площадь прямоугольника BCNK = BC • BK = 2 см • 2 см = 4 см2.
Сумма площадей прямоугольников AMBK и CPDN равна разности площадей прямоугольников AMPD и BCNK = 10 см2 — 4 см2 = 6 см2.
Сумма площадей треугольников ABK и CDN = Сумма площадей прямоугольников AMBK и CPDN : 2 = 6 см2 : 2 = 3 см2.
Площадь трапеции ABCD = Площадь прямоугольника BCNK + сумма площадей треугольников ABK и CDN = 4 см2 + 3 см2 = 7 см2.
| ← Предыдущая | Следующая → |
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.