Алгебраические выражения
Формулы сокращённого умножения
Квадрат разности
Ответы к стр. 103
351. Запишите и прочитайте формулу квадрата разности.
(α − b)2 = α2 − 2αb + b2
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого и второго чисел плюс квадрат второго числа.
352. Преобразуйте выражение в многочлен стандартного вида двумя способами:
а) (α − b)2; б) (x − 3)2; в) (1 − m)2; г) (5 + p)2;
д) (2α − 3)2; е) (4 − 3y)2; ж) (3m + 2n)2; з) (5p − 2q)2.
а) (α − b)2 = (α − b)(α − b) = α2 – αb – αb + b2 = α2 − 2αb + b2,
(α − b)2 = α2 − 2αb + b2;
б) (x − 3)2 = (x − 3)(x − 3) = x2 − 3x − 3x + 9 = x2 − 6x + 9,
(x − 3)2 = x2 − 2•x•3 + 32 = x2 − 6x + 9;
в) (1 − m)2 = (1 − m)(1 − m) = 1 – m – m + m2 = 1 − 2m + m2,
(1 − m)2 = 12 − 2•1•m + m2 = 1 − 2m + m2;
г) (5 + p)2 = (5 + p)(5 + p) = 25 + 5p + 5p + p2 = 25 + 10p + p2,
(5 + p)2 = 52 + 2•5•p + p2 = 25 + 10p + p2;
д) (2α − 3)2 = (2α − 3)(2α − 3) = 4α2 − 6α − 6α + 9 = 4α2 − 12α + 9,
(2α − 3)2 = (2α)2 − 2•2α•3 + 32 = 4α2 − 12α + 9;
е) (4 − 3y)2 = (4 − 3y)(4 − 3y) = 16 − 12y − 12y + 9y2 = 16 − 24y + 9y2,
(4 − 3y)2 = 42 − 2•4•3y + (3y)2 = 16 − 24y + 9y2;
ж) (3m + 2n)2 = (3m + 2n)(3m + 2n) = 9m2 + 6mn + 6mn + 4n2 = 9m2 + 12mn + 4n2,
(3m + 2n)2 = (3m)2 + 2•3m•2n + (2n)2 = 9m2 + 12mn + 4n2;
з) (5p − 2q)2 = (5p − 2q)(5p − 2q) = 25p2 − 10pq − 10pq + 4q2 = 25p2 − 20pq + 4q2,
(5p − 2q)2 = (5p)2 − 2•5p•2q + (2q)2 = 25p2 − 20pq + 4q2.
353. Используя формулу квадрата суммы или разности, преобразуйте выражение в многочлен стандартного вида:
а) (α − b2)2; б) (x3 − y)2; в) (m3 − n2)2;
г) (p4 + q2)2; д) (α3 + αb)2; е) (x3 − y2z)2;
ж) (2m − n2)2; з) (3p2 − 2q3)2; и) (4α2b − 3αb2)2.
а) (α − b2)2 = α2 − 2•α•b2 + (b2)2 = α2 − 2αb2 + b4;
б) (x3 − y)2 = (x3)2 − 2•x3•y + y2 = x6 − 2x3y + y2;
в) (m3 − n2)2 = (m3)2 − 2•m3•n2 + (n2)2 = m6 − 2m3n2 + n4;
г) (p4 + q2)2 = (p4)2 + 2•p4•q2 + (q2)2 = p8 + 2p4q2 + q4;
д) (α3 + αb)2 = (α3)2 + 2•α3•αb + (αb)2 = α6 + 2α4αb + α2b2;
е) (x3 − y2z)2 = (x3)2 − 2•x3•y2z + (y2z)2 = x6 − 2x3y2z + y4z2;
ж) (2m − n2)2 = (2m)2 − 2•2m•n2 + (n2)2 = 4m2 − 4mn2 + n4;
з) (3p2 − 2q3)2 = (3p2)2 − 2•3p2•2q3 + (2q3)2 = 9p4 − 12p2q3 + 4q6;
и) (4α2b − 3αb2)2 = (4α2b)2 − 2•4α2b•3αb2 + (3αb2)2 = 16α4b2 − 24α3b3 + 9α2b4.
354. Преобразуйте выражение в многочлен:
а) (1/5 mn − m3)2; б) (−1/2 + 3bc)2;
в) (1/2 x3 – 1/3 y4)2; г) (−11/2 p2 + 2/3 q)2;
д) (11/3 αb2 − 3α2b)2; е) (2m3n2 – 21/2 mn3)2;
ж) (0,1α + 3α2b)2; з) (1,2xy + 0,7x2)2;
и) (−0,5x3y2 + 0,3xy5)2.
а) (1/5 mn − m3)2 = (1/5 mn)2 − 2•1/5 mn•m3 + (m3)2 = 1/25 m2n2 – 2/5 m4n + m6;
б) (−1/2 + 3bc)2 = (−1/2)2 + 2•(−1/2)•3bc + (3bc)2 = 1/4 − 3bc + 9b2c2;
в) (1/2 x3 – 1/3 y4)2 = (1/2 x3)2 − 2•1/2 x3•1/3 y4 + (1/3 y4)2 = 1/4 x6 – 1/3 x3y4 + 1/9 y8;
г) (−11/2 p2 + 2/3 q)2 = (−3/2 p2)2 + 2•(−3/2 p2)•2/3 q + (2/3 q)2 = 9/4 p4 − 2p2q + 4/9 q2 = 21/4 p4 − 2p2q + 4/9 q2;
д) (11/3 αb2 − 3α2b)2 = (4/3 αb2)2 − 2•4/3 αb2•3α2b + (3α2b)2 = 16/9 α2b4 − 8α3b3 + 9α4b2 = 17/9 α2b4 − 8α3b3 + 9α4b2;
е) (2m3n2 – 21/2 mn3)2 = (2m3n2)2 − 2•2m3n2•5/2 mn3 + (5/2 mn3)2 = 4m6n4 − 10m4n5 + 25/4 m2n6 = 4m6n4 − 10m4n5 + 61/4 m2n6;
ж) (0,1α + 3α2b)2 = (0,1α)2 + 2•0,1α•3α2b + (3α2b)2 = 0,01α2 + 0,6α3b + 9α4b2;
з) (1,2xy + 0,7x2)2 = (1,2xy)2 + 2•1,2xy•0,7x2 + (0,7x2)2 = 1,44x2y2 + 1,68x3y + 0,49x4;
и) (−0,5x3y2 + 0,3xy5)2 = (−0,5x3y2)2 + 2•(−0,5x3y2)•0,3xy5 + (0,3xy5)2 = 0,25x6y4 − 0,3x4y7 + 0,09x2y10.
355. Доказываем. Пользуясь рисунком 14, докажите формулу квадрата разности для α > 0, b > 0, α > b.
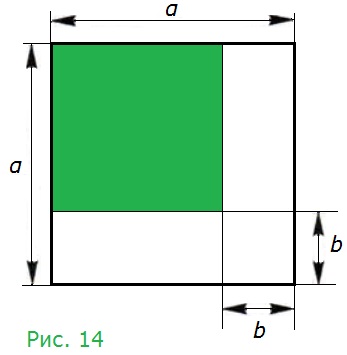
α•α = α2 − площадь всего квадрата,
b•b = b2 − площадь малого квадрата,
(α − b)(α − b) = (α − b)2 − площадь зелёного квадрата,
(α − b)b = αb − b2 − площадь каждого из двух прямоугольников.
Тогда площадь зелёного квадрата: (α − b)2 = α2 − b2 − (αb − b2) − (αb − b2) = α2 − b2 – αb + b2 – αb + b2 = α2 − 2αb + b2.
356. Вычислите, применив формулу квадрата разности:
а) 492; б) 892;
в) 1992; г) 382;
д) 982; е) 1982.
а) 492 = (50 − 1)2 = 502 − 2•50•1 + 12 = 2500 – 100 + 1 = 2401;
б) 892 = (90 − 1)2 = 902 − 2•90•1 + 12 = 8100 – 180 + 1 = 7921;
в) 1992 = (200 − 1)2 = 2002 − 2•200•1 + 12 = 40 000 – 400 + 1 = 39 601;
г) 382 = (40 − 2)2 = 402 − 2•40•2 + 22 = 1600 – 160 + 4 = 1444;
д) 982 = (100 − 2)2 = 1002 − 2•100•2 + 22 = 10 000 – 400 + 4 = 9604;
е) 1982 = (200 − 2)2 = 2002 − 2•200•2 + 22 = 40 000 – 800 + 4 = 39 204.
357. Представьте многочлен в виде квадрата разности:
а) α2 − 2αb + b2; б) 4x2 − 4xy + y2;
в) 9m2 − 6m + 1; г) 25 − 30c + 9c2;
д) 16p2 − 56pq + 49q2; е) 100α2 + 25b2 − 100αb;
ж) x4 − 6x2y + 9y2; з) 16 + 9x6 − 24x3.
а) α2 − 2αb + b2 = (α − b)2;
б) 4x2 − 4xy + y2 = (2x)2 − 2•2x•y + y2 = (2x − y)2;
в) 9m2 − 6m + 1 = (3m)2 − 2•3m•1 + 12 = (3m − 1)2;
г) 25 − 30c + 9c2 = 52 − 2•5•3c + (3c)2 = (5 − 3c)2;
д) 16p2 − 56pq + 49q2 = (4p)2 − 2•4p•7q + (7q)2 = (4p − 7q)2;
е) 100α2 + 25b2 − 100αb = 100α2 − 100αb + 25b2 = (10α)2 − 2•10α•5b + (5b)2 = (10α − 5b)2;
ж) x4 − 6x2y + 9y2 = (x2)2 − 2•x2•3y + (3y)2 = (x2−3y)2;
з) 16 + 9x6 − 24x3 = 16 − 24x3 + 9x6 = 42 − 2•4•3x3 + (3x3)2 = (4 − 3x3)2.
| ← Предыдущая | Следующая → |