Алгебраические выражения
Многочлены
Произведение многочленов
Ответы к стр. 90
Выполните умножение (294 — 295):
295. а) (5m + 7n)(2n + 4m); б) (12α + b)(3α + 5b);
в) (2x − 3y)(2x + 3y); г) (5m − 2n)(3n − 5m);
д) (−α − b)(2α − 3b); е) (−7x − 4y)(−5x + 7y);
ж) (α2 + b2)(α2 + b2); з) (mn3 − m2)(m − 1);
и) (2x2 − y2)(y2 + 2x3); к) (xy2 + 3α2)(3xy + α3).
а) (5m + 7n)(2n + 4m) = 10mn + 14n2 + 20m2 + 28mn = 20m2 + 14n2 + 38mn;
б) (12α + b)(3α + 5b) = 36α2 + 3αb + 60αb + 5b2 = 36α2 + 5b2 + 63αb;
в) (2x − 3y)(2x + 3y) = 4x2 − 6xy + 6xy − 9y2 = 4x2 − 9y2;
г) (5m − 2n)(3n − 5m) = 15mn − 6n2 − 25m2 + 10mn = −25m2 − 6n2 + 25mn;
д) (−α − b)(2α − 3b) = −2α2 − 2αb + 3αb + 3b2= −2α2 + 3b2 + αb;
е) (−7x − 4y)(−5x + 7y) = 35x2 + 20xy − 49xy − 28y2 = 35x2 − 28y2 − 29xy;
ж) (α2 + b2)(α2 + b2) = α4 + α2b2 + α2b2 + b4 = α4 + 2α2b2 + b4;
з) (mn3 − m2)(m − 1) = m2n3 − m3 − mn3 + m2;
и) (2x2 − y2)(y2 + 2x3) = 2x2y2 − y4 + 4x5 − 2x3y2;
к) (xy2 + 3α2)(3xy + α3) = 3x2y3 +9α2xy + α3xy2 +3α5.
Преобразуйте произведение многочленов в многочлен стандартного вида (296 — 300):
296. а) (α + 1)(α + 1)(α + 1); б) (x − 1)(x − 1)(x − 1);
в) (α + b)(α − b)(α + b); г) (m − n)(m − n)(m + n);
д) (α + b + c)(α + 1); е) (α − b − c)(α − 1);
ж) (x + 1)(x2 – x + 1); з) (x − 1)(x2 + x + 1);
и) (x3 + 2x − 3)(2 − 3x); к) (5m2 − 3mn + n2)(2n − m2);
л) (α + b + c)(α + b − c); м) (α − b + c)(α − b − c).
а) (α + 1)(α + 1)(α + 1) = (α2 + α + α + 1)(α + 1) = (α2 + 2α + 1)(α + 1) = α3 + 2α2 + α + α2 + 2α + 1 = α3 + 3α2 + 3α + 1;
б) (x − 1)(x − 1)(x − 1) = (x2 – x – x + 1)(x − 1) = (x2 − 2x + 1)(x − 1) = x3 − 2x2 + x − x2 + 2x – 1 = x3 − 3x2 + 3x – 1;
в) (α + b)(α − b)(α + b) = (α2 + αb – αb − b2)(α + b) = (α2 − b2)(α + b) = α3 + α2b − αb2 − b3;
г) (m − n)(m − n)(m + n) = (m2 – mn – mn + n2)(m + n) = (m2 − 2mn + n2)(m + n) = m3 − 2m2n + mn2 + m2n − 2mn2 + n3 = m3 − m2n − mn2 + n3;
д) (α + b + c)(α + 1) = α2 + αb + αc + α + b + c;
е) (α − b − c)(α − 1) = α2 – αb – αc – α + b + c;
ж) (x + 1)(x2 – x + 1) = x3 − x2 + x + x2 – x + 1 = x3 + 1;
з) (x − 1)(x2 + x + 1) = x3 + x2 + x −x2 – x – 1 = x3 − 1;
и) (x3 + 2x − 3)(2 − 3x) = 2x3 + 4x – 6 − 3x4 − 6x2 + 9x = −3x4 + 2x3 − 6x2 + 13x − 6;
к) (5m2 − 3mn + n2)(2n − m2) = 10m2n −6mn2 + 2n3 −5m4 + 3m3n − m2n2;
л) (α + b + c)(α + b − c) = α2 + αb + αc + αb + b2 + bc – αc – bc − c2 = α2 + 2αb + b2 − c2;
м) (α − b + c)(α − b − c) = α2 – αb + αc – αb + b2 – bc – αc + bc − c2 = α2 − 2αb + b2 − c2.
297. а) −(α + b)(α + b); б) −(x − y)(x + y);
в) −(x − y)(x − y); г) −(2m − n)(n − 3m);
д) −(5α − 2b)(3b + 2α); е) −7(x + 8y)(y − 3x).
а) −(α + b)(α + b) = −(α2 + αb + αb + b2) = −(α2 + 2αb + b2) = −α2 − 2αb − b2;
б) −(x − y)(x + y) = −(x2 – xy + xy − y2) = −(x2 − y2) = −x2 + y2;
в) −(x − y)(x − y) = −(x2 – xy – xy + y2) = −(x2 − 2xy + y2) = −x2 + 2xy − y2;
г) −(2m − n)(n − 3m) = −(2mn − n2 − 6m2 + 3mn) = −(−n2 − 6m2 + 5mn) = n2 + 6m2 − 5mn;
д) −(5α − 2b)(3b + 2α) = −(15αb − 6b2 + 10α2 − 4αb) = −(10α2 + 11αb − 6b2) = −10α2 − 11αb + 6b2;
е) −7(x + 8y)(y − 3x) = −7(xy + 8y2 − 3x2 − 24xy) = −7(8y2 − 3x2 − 23xy) = −56y2 + 21x2 + 161xy.
298. а) (8x − 3)(4x + 5); б) 8x − 3 • 4x + 5;
в) (4α − 3) • 2α − 3; г) 4α − 3(2α − 3).
а) (8x − 3)(4x + 5) = 32x2 − 12x + 40x – 15 = 32x2 + 28x – 15;
б) 8x − 3 • 4x + 5 = 8x − 12x + 5 = −4x + 5;
в) (4α − 3) • 2α – 3 = 8α2 − 6α – 3;
г) 4α − 3(2α − 3) = 4α − 6α + 9 = −2α + 9.
299. а) (0,1 − x)(x + 0,1); б) (1,2 − α)(1,2 + α);
в) (1/3 − m)(1/2 m − 3); г) (1/5 α – 3/7 b)(14α + b);
д) (0,05y − 2,3x)(y − 0,2x); е) (2,5α + 3b)(0,1b − 4α);
ж) (2/3 m + 3n)(6m – 1/6 n); з) (11/2 x − y)(21/3 y – 1/3 x).
а) (0,1 − x)(x + 0,1) = 0,1x − x2 + 0,01 − 0,1x = −x2 + 0,01;
б) (1,2 − α)(1,2 + α) = 1,44 − 1,2α + 1,2α − α2 = 1,44 − α2;
в) (1/3 − m)(1/2 m − 3) = 1/6 m – 1/2 m2 – 1 + 3m = 31/6 m – 1/2 m2 − 1;
г) (1/5 α – 3/7 b)(14α + b) = 24/5 α2 − 6αb + 1/5 αb – 3/7 b2 = 24/5 α2 − 54/5 αb − 3/7 b2;
д) (0,05y − 2,3x)(y − 0,2x) = 0,05y2 − 2,3xy − 0,01xy + 0,46x2 = 0,05y2 − 2,31xy + 0,46x2;
е) (2,5α + 3b)(0,1b − 4α) = 0,25αb + 0,3b2 − 10α2 − 12αb = 0,3b2 − 10α2 − 11,75αb;
ж) (2/3 m + 3n)(6m – 1/6 n) = 4m2 + 18mn − 1/9 mn − 1/2 n2 = 4m2 + 178/9 mn – 1/2 n2;
з) (11/2 x − y)(21/3 y – 1/3 x) = (3/2 x − y)(7/3 y – 1/3 x) = 7/2 xy – 7/3 y2 – 1/2 x2 + 1/3 xy = 21/6 xy – 7/3 y2 – 1/2 x2 + 2/6 xy = 23/6 xy – 7/3 y2 – 1/2 x2 = 35/6 xy – 21/3 y2 – 1/2 x2.
300. а) (α + 2b)(α2 − 2αb + 4b2); б) (α − b + c)(α + b − c);
в) (α + 2b)(α − 2b)(α2 + 4b2).
а) (α + 2b)(α2 − 2αb + 4b2) = α3 + 2α2b − 2α2b − 4αb2 + 4αb2 + 8b3 = α3 + 8b3;
б) (α − b + c)(α + b − c) = α2 – αb + αc + αb − b2 + bc – αc + bc − c2 = α2 − b2 + 2bc − c2;
в) (α + 2b)(α − 2b)(α2 + 4b2) = (α2 + 2αb − 2αb − 4b2)(α2 + 4b2) = (α2 − 4b2)(α2 + 4b2) = α4 − 4α2b2 + 4α2b2 − 16b4 = α4 − 16b4.
301. Доказываем. Докажите равенство:
а) (α + b)(α + c) = α2 + (b + c)α + bc;
б) 2x2 − 11x + 15 = (x − 3)(2x − 5).
а) (α + b)(α + c) = α2 + αb + αc + bc,
α2 + (b + c)α + bc = α2 + αb + αc + bc,
так как α2 + αb + αc + bc = α2 + αb + αc + bc, то (α + b)(α + c) = α2 + (b + c)α;
б) (x − 3)(2x − 5) = 2x2 − 6x − 5x + 15 = 2x2 − 11x + 15,
так как 2x2 − 11x + 15 = 2x2 − 11x + 15, то 2x2 − 11x + 15 = (x − 3)(2x − 5).
302. Верно ли выполнены преобразования:
а) (2x + 3y)(3x − 2y) = 6x2 − 4xy + 9xy − 6y2 = 6x2 + 5xy − 6y2;
б) (xy2 + x2y)(xy + 3) = x2y3 + 3xy2 + x3y2 + 3x2y?
а) преобразования выполнены верно;
б) преобразования выполнены верно.
303. Вместо звёздочки подберите одночлен, чтобы выполнялось равенство:
а) (α + ∗)(α − b) = α2 – αb + αb − b2;
б) 9 − 3α − 3α + α2 = 9 − ∗ + α2.
а) α2 – αb + αb − b2 = (α2 – αb) + (αb − b2) = α(α – b) + b(α – b) = (α – b)(α + b), то есть (α + ∗)(α − b) = (α + b)(α − b), следовательно, ∗ = b;
б) 9 − 3α − 3α + α2 = 9 − 6α + α2, то есть 9 − 6α + α2 = 9 − ∗ + α2, следовательно, ∗ = 6α.
304. Доказываем. Пользуясь рисунком 12, докажите, что для α > 0, b > 0, c > 0, d > 0 верно равенство (α + b)(c + d) = αc + bc + αd + bd.
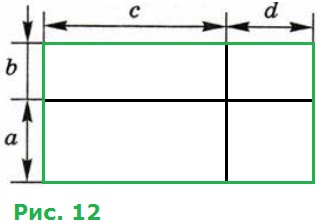
Большой прямоугольник состоит их четырёх маленьких прямоугольников: α + b − ширина всего прямоугольника, c + d − длина всего прямоугольника,
(α + b)(c + d) − площадь всего прямоугольника.
Тогда:
αc − площадь левого нижнего прямоугольника;
bc − площадь левого верхнего прямоугольника;
αd − площадь правого нижнего прямоугольника;
bd − площадь правого верхнего прямоугольника.
Площадь всего прямоугольника равна сумме площадей прямоугольников, его составляющих, следовательно: (α + b)(c + d) = αc + bc + αd + bd.
| ← Предыдущая | Следующая → |