Начальные геометрические сведения
Сравнение отрезков и углов
Равенство геометрических фигур. Сравнение отрезков и углов
Ответы к стр. 12
18. На луче с началом О отмечены точки А, В и С так, что точка В лежит между точками О и А, а точка А — между точками О и С. Сравните отрезки OB и ОА, ОС и OA, OB и OC.
![]()
Выражение «точка B лежит между точками О и А» можно записать так: О – В – А. Для точки А: О — А — С. Из записи видно, что общее расположение точек: О — В — А — С.
Отрезок ОВ составляет часть отрезка ОА (О — В — А), следовательно, ОВ < ОА.
Отрезок ОА составляет часть отрезка ОС (О — А — С), следовательно, ОС > ОА.
Отрезок ОВ составляет часть отрезка ОС (О — В — С), следовательно, ОВ < ОС.
19. Точка О является серединой отрезка AB. Можно ли совместить наложением отрезки: а) ОА и OB; б) ОА и AB?
а) точка О делит отрезок АВ на два равных отрезка, то есть отрезок AO равен отрезку ОВ, следовательно, эти отрезки при наложении совместятся;
б) отрезок ОА составляет часть отрезка АВ, следовательно, эти отрезки при наложении не совместятся, так как ОА < АВ.
20. На рисунке 25 отрезки AB, BC, CD и DE равны. Укажите: а) середины отрезков AC, AE и CE; б) отрезок, серединой которого является точка D; в) отрезки, серединой которых является точка С.
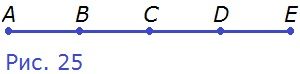
а) АС = АВ + ВС, АВ = ВС, следовательно, точка В — середина отрезка АС;
АЕ = АС + СЕ, АС = АВ + ВС, СЕ = СD + DЕ, АВ + ВС = СD + DЕ или АС = СЕ, следовательно, точка С — середина отрезка АЕ;
СЕ = СD + DЕ, СD = DЕ, следовательно, точка D — середина отрезка СЕ;
б) точка D принадлежит отрезкам СD и DЕ, СD = DЕ, СD + DЕ = СЕ, следовательно, точка D является серединой отрезка СЕ;
в) точка С принадлежит отрезкам ВС и СD, ВС = СD, ВС + СD = ВD, следовательно, точка С является серединой отрезка ВD;
точка С принадлежит отрезкам АС и СЕ, АС = АВ + ВС, СЕ = СD + DЕ, АВ + ВС = СD + DЕ или АС = СЕ, АС + СЕ = АЕ, следовательно, точка С является серединой отрезка АЕ.
| ← Предыдущая | Следующая → |