Начальные геометрические сведения
Измерение отрезков
Длина отрезка. Единицы измерения. Измерительные инструменты
Ответы к стр. 17
Задачи
30. Точка В делит отрезок АС на два отрезка. Найдите длину отрезка АС, если АВ = 7,8 см, ВС = 25 мм.
Д а н о
А — В — С
АВ = 7,8 см
ВС = 25 мм
Н а й т и
АС — ?
Р е ш е н и е
АС = АВ + ВС
ВС = 25 мм = 2,5 см
АС = 7,8 + 2,5 = 10,3 (см)
О т в е т. АС = 10,3 см.
31. Точка В делит отрезок АС на два отрезка. Найдите длину отрезка ВС, если: а) АВ = 3,7 см, АС = 7,2 см; б) AB = 4 мм, АС = 4 см.
а) Д а н о
А — В — С
АВ = 3,7 см
АС = 7,2 см
Н а й т и
ВС — ?
Р е ш е н и е
АС = АВ + ВС ⇒ ВС = АС — АВ
ВС = 7,2 — 3,7 = 3,5 (см)
О т в е т. ВС = 3,5 см.
б) Д а н о
А — В — С
АВ = 4 мм
АС = 4 см
Н а й т и
ВС — ?
Р е ш е н и е
АС = АВ + ВС ⇒ ВС = АС — АВ
АС = 4 см = 40 мм
ВС = 40 — 4 = 36 (мм)
О т в е т. ВС = 36 мм.
32. Точки А, B и С лежат на одной прямой. Известно, что AB = 12 см, BC = 13,5 см. Какой может быть длина отрезка АС?
Д а н о
А, В, С ∈ α
АВ = 12 см
ВС = 13,5 см
Н а й т и
АС — ?
Р е ш е н и е.
Рассмотрим взаимное расположение точек: А — В — С или В — А — С (А — С — В быть не может, так как по условию задачи АВ < ВС).
а) Для А — В — С:
АС = АВ + ВС
АС = 12 + 13,5 = 25,5 (см)
б) Для В — А — С:
ВС = АВ + АС ⇒ АС = ВС — АВ
АС = 13,5 — 12 = 1,5 (см)
О т в е т. Длина отрезка АС может быть 25,5 см или 1,5 см.
33. Точки B, D и М лежат на одной прямой. Известно, что BD = 7 см, MD = 16 см. Каким может быть расстояние BM?
Д а н о
В, D, М ∈ α
ВD = 7 см
MD = 16 см
Н а й т и
ВМ — ?
Р е ш е н и е.
Рассмотрим взаимное расположение точек: В — D — М или D — В — М (В — М — D быть не может, так как по условию задачи ВD < MD).
а) Для В — D — М:
BM = ВD + MD
BM = 7 + 16 = 23 (см)
б) Для D — В — М:
MD = BD + BM ⇒ BM = MD — BD
BM = 16 — 7 = 9 (см)
О т в е т. Расстояние BM может быть 23 см или 9 см.
34. Точка С — середина отрезка AB, равного 64 см. На луче СА отмечена точка D так, что CD = 15 см. Найдите длины отрезков BD и DA.
Д а н о
А — С — В
АС = ВС
АВ = 64 см
D ∈ СА
СD = 15 см
Н а й т и
ВD — ?
DA — ?
Р е ш е н и е.
AC = BC = AB : 2 = 64 : 2 = 32 (см)
АС = 32 см, СD = 15 см ⇒ АС > СD и расположение точек будет: A — D — C — B
АС = АD + СD ⇒ DA = AC — CD = 32 — 15 = 17 (см)
АВ = АD + DB ⇒ BD = AB — DА = 64 — 17 = 47 (см) или
BD = CD + BC = 15 + 32 = 47 (см)
О т в е т. Длина отрезка BD = 47 см, отрезка DA = 17 см.
35. Расстояние между Москвой и С.-Петербургом равно 650 км. Город Тверь находится между Москвой и С.-Петербургом в 170 км от Москвы. Найдите расстояние между Тверью и С.-Петербургом, считая, что все три города расположены на одной прямой.
Д а н о
Москва — С.-Петербург = 650 км
Москва — Тверь — С.-Петербург
Москва — Тверь = 170 км
Н а й т и
Тверь — С.-Петербург = ?
Р е ш е н и е.
Москва — т. М, Тверь — т. Т, С.-Петербург — т. S
Расположение точек на прямой: М — Т — S
MS = MT + TS ⇒ TS = MS — MT = 650 — 170 = 480 (км)
О т в е т. Расстояние между Тверью и С.-Петербургом 480 км.
36. Лежат ли точки А, B и С на одной прямой, если АС = 5 см, AB = 3 см, BC = 4 см?
Д а н о
АС = 5 см
АВ = 3 см
ВС = 4 см
В е р н о: А, В, С ∈ α?
Р е ш е н и е.
Если точки А, В и С лежат на одной прямой, то больший из отрезков АВ, ВС и АС равен сумме двух других. По условию больший из из данных отрезков (отрезок АС) равен 5 см, а сумма двух других (АВ + ВС) равна 7 см. Поэтому точки А, В и С не лежат на одной прямой.
О т в е т. А, В и С не лежат на одной прямой.
37. Точка С — середина отрезка AB, точка О — середина отрезка АС. Найдите:
а) АС, СB, АО и ОB, если AB = 2 см;
б) AB, АС, АО и ОB, если СB = 3,2 м.
Д а н о
С ∈ АВ
АС = СВ
О ∈ АС
АО = ОС
Н а й т и
а) АС, СB, АО и ОB, если AB = 2 см;
б) AB, АС, АО и ОB, если СB = 3,2 м.
Р е ш е н и е
а) Расположение точек: А — О — С — В
AC = CВ = AB : 2 = 2 : 2 = 1 (см)
АО = ОС = АС : 2 = 1 : 2 = 0,5 (см)
ОВ = ОС + СВ = 0,5 + 1 = 1,5 (см)
О т в е т. АС = 1 см, СB = 1 см, АО = 0,5 см, ОB = 1,5 см.
б) Расположение точек: А — О — С — В
СВ = АВ : 2 ⇒ АВ = 2СВ = 2 • 3,2 = 6,4 (м)
АС = CB = 3,2 м
АО = ОС = АС : 2 = 3,2 : 2 = 1,6 (м)
ОВ = ОС + СВ = 1,6 + 3,2 = 4,8 (м)
О т в е т. АВ = 6,4 см, АС = 3,2 см, АО = 1,6 см, ОB = 4,8.
38. На прямой отмечены точки О, А и B так, что ОА = 12 см, ОB = 9 см. Найдите расстояние между серединами отрезков ОА и ОB, если точка О:
а) лежит на отрезке AB;
б) не лежит на отрезке AB.
Д а н о
О, А, В ∈ α
ОА = 12 см
ОВ = 9 см
Н а й т и
Расстояние между серединами ОА и ОВ, если:
а) О ∈ АВ;
б) О ∉ АВ.
Р е ш е н и е
а) Расположение точек: А — О — В
Дополнительные построения: т. С — середина ОА, т. Е — середина ОВ
![]()
АС = СО = АО : 2 = 12 : 2 = 6 (см)
ВЕ = ЕО = ВО : 2 = 9 : 2 = 4,5 (см)
Тогда: А — С — О — Е — В, расстояние между серединами ОА и ОВ — отрезок СЕ.
СЕ = СО + ОЕ = 6 + 4,5 = 10,5 (см)
О т в е т. Расстояние между серединами ОА и ОВ 10,5 см.
б) Расположение точек: О — В — А (О — А — В быть не может, так как по условию задачи ОА > ОВ).
Дополнительные построения: т. С — середина ОА, т. Е — середина ОВ

АС = СО = АО : 2 = 12 : 2 = 6 (см)
ВЕ = ЕО = ВО : 2 = 9 : 2 = 4,5 (см)
Так как СО > ЕО, то Е ∈ СО
Тогда: О — В — С — Е — А, расстояние между серединами ОА и ОВ — отрезок СЕ.
СО = СЕ + ЕО ⇒ СЕ = СО — ЕО = 6 — 4,5 = 1,5 (см)
О т в е т. Расстояние между серединами ОА и ОВ 1,5 см.
39. Отрезок, длина которого равна α, разделен произвольной точкой на два отрезка. Найдите расстояние между серединами этих отрезков.
Д а н о
A — B — С
АС = α
Е — середина АВ
Р — середина ВС
Н а й т и
ЕР = ?
Р е ш е н и е
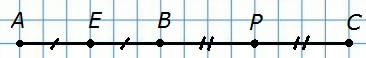
Расположение точек: А — Е — В — Р — С
АЕ = ЕВ = 1/2 АB
ВР = РС = 1/2 ВС
ЕР = ЕВ + ВР = 1/2 АВ + 1/2 ВС = 1/2 (АВ + ВС) = 1/2 АС = 1/2 α
О т в е т. ЕР = 1/2 α.
40. Отрезок, равный 28 см, разделён на три неравных отрезка. Расстояние между серединами крайних отрезков 16 см. Найдите длину среднего отрезка.
Д а н о
A — С — Е — B
АВ = 28 см
Р — середина АС
М — середина ЕВ
РМ = 16 см
Н а й т и
СЕ = ?
Р е ш е н и е

Расположение точек: А — Р — С — Е — М — В
АР + МВ = АВ — РМ = 28 — 16 = 12 (см)
АР = РС, МВ = ЕМ ⇒ АР + МВ = РС + ЕМ
АР + МВ + РС + ЕМ = 12 + 12 = 24 (см)
СЕ = АВ — (АР + МВ + РС + ЕМ) = 28 — 24 = 4 (см)
О т в е т. СЕ = 4 см.
| ← Предыдущая | Следующая → |