Треугольники
Медианы, биссектрисы и высоты треугольника
Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Свойства равнобедренного треугольника
Ответы к стр. 36
Практические задания
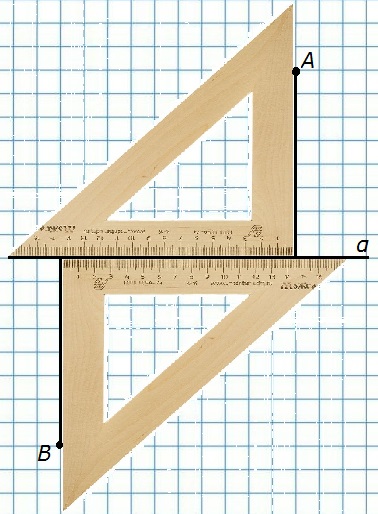
100. Начертите прямую α и отметьте точки А и B, лежащие по разные стороны от прямой α. С помощью чертежного угольника проведите из этих точек перпендикуляры к прямой α.
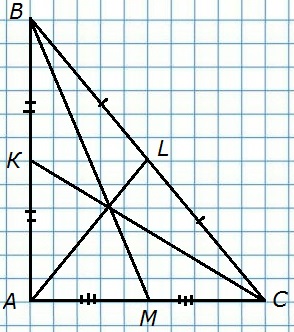
101. Начертите треугольник. С помощью масштабной линейки отметьте середины сторон и проведите медианы треугольника.
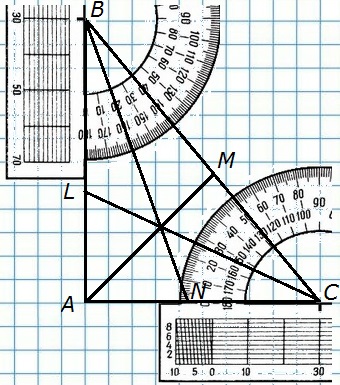
102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.
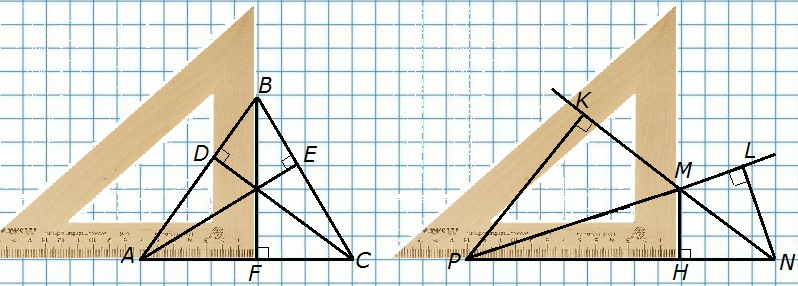
103. Начертите треугольник ABC с тремя острыми углами и треугольник MNP, у которого угол М тупой. С помощью чертежного угольника проведите высоты каждого треугольника.
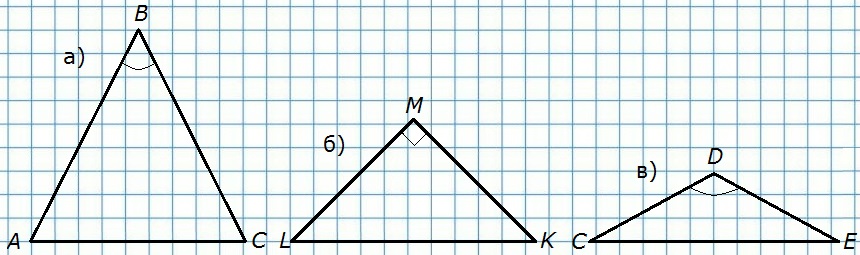
104. Начертите три равнобедренных треугольника так, чтобы угол, лежащий против основания, был: а) острым; б) прямым; в) тупым.
Задачи
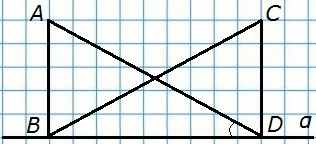
105. Точки А и С лежат по одну сторону от прямой α. Перпендикуляры АВ и CD к прямой α равны.
а) Докажите, что ∠ABD = ∠CDB;
б) найдите ∠ABC, если ∠ADB = 44°.
Д а н о
АВ, СD ⊥ α
АВ = СD
а) Д о к а з а т ь
∠АВD = ∠CDВ
б) Н а й т и
∠АBС — ? если ∠ADB = 44°
Р е ш е н и е
а) АВ ⊥ α, следовательно, ∠АВD = 90°.
СD ⊥ α, следовательно, ∠CDВ = 90°.
Тогда ∠АВD = ∠CDВ = 90°.
б) ВD ∈ ΔАВD, ВD ∈ ΔCDВ, следовательно, ВD — общая сторона для ΔАВD и ΔCDВ. АВ = CD — по условию, ∠АВD = ∠CDВ. Следовательно, ΔАВD = ΔCDВ по первому признаку равенства треугольников (по двум сторонам и углу между ними).
ΔАВD = ΔCDВ, следовательно, ∠АDВ = ∠СBD = 44°. Тогда ∠АВС = ∠ABD — ∠CBD = 90° — 44° = 46°.
О т в е т: а) ∠АВD = ∠CDВ, б) ∠АВС = 46°.
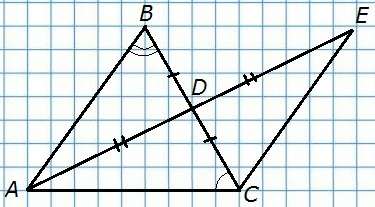
106. Медиана AD треугольника ABC продолжена за сторону ВС на отрезок DE, равный AD, и точка Е соединена с точкой С.
а) Докажите, что ΔABD = ΔECD;
б) найдите ∠ACE, если ∠ACD = 56°, ∠ABD = 40°.
Д а н о
ΔАВС
АD — медиана ΔАВС
АD = DE
а) Д о к а з а т ь
ΔАВD = ΔECD
б) Н а й т и
∠АСE — ? если ∠ACD = 56°, ∠ABD = 40°.
Р е ш е н и е
а) АD = DE — по условию, т. D — середина BC, значит ВD = DC. По определению вертикальных углов ∠АDВ = ∠CDE. Следовательно, ΔАВD = ΔECD по первому признаку равенства треугольников (по двум сторонам и углу между ними).
б) ∠АСE = ∠ACD + ∠DCE. Так как ΔАВD = ΔECD, то ∠DCE = ∠АВD = 40°. Тогда ∠АСE = 56° + 40° = 96°.
О т в е т: а) ΔАВD = ΔECD, б) ∠АСE = 96°.
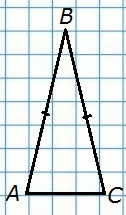
107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметр равен 50 см. Найдите стороны треугольника.
Д а н о
ΔАВС
АВ = ВС
АС = 1/2 АВ
РΔАВС = 50 см
Н а й т и
АВ, ВС, АС — ?
Р е ш е н и е
РΔАВС = АВ + ВС + АС
АВ = ВС, АС = 1/2 АВ, тогда:
РΔАВС = АВ + ВС + АС = АВ + АВ + 1/2 АВ
АВ + АВ + 1/2 АВ = 50
21/2 АВ = 50
АВ = 50 : 21/2
АВ = 20 (см)
АВ = ВС = 20 см
АС = 1/2 • 20 = 10 (см)
О т в е т: АВ = 20 см, ВС = 20 см, АС = 10 см.
108. Периметр равнобедренного треугольника ABC с основанием ВС равен 40 см, а периметр равностороннего треугольника BCD равен 45 см. Найдите стороны АВ и ВС.
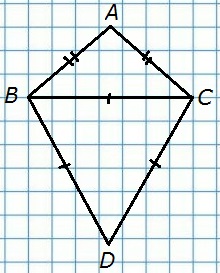
Д а н о
ΔАВС
АВ = АС
РΔАВС = 40 см
ΔВСD
BС = CD = BD
РΔВСD = 45 см
Н а й т и
АВ, ВС — ?
Р е ш е н и е
РΔВСD = BС + CD + BD
Так как BС = CD и BС = BD, то РΔВСD = ВС + ВС + ВС = 3BС
3ВС = 45
ВС = 45 : 3
ВС = 15 (см)
РΔАВС = АВ + АС + ВС
Так как АВ = АС и ВС = 15 см, то РΔАВС = АВ + АВ + 15 = 2АВ + 15
2АВ + 15 = 40
2АВ = 40 — 15
2АВ = 25
АВ = 25 : 2
АВ = 12,5 (см)
О т в е т: АВ = 12,5 см, ВС = 15 см.
109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника АВМ равен 24 см.
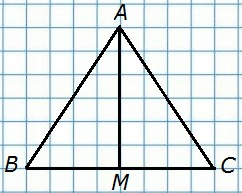
Д а н о
ΔАВС
АВ = АС
АМ — медиана
РΔАВС = 32 см
РΔАВМ = 24 см
Н а й т и
АМ — ?
Р е ш е н и е
РΔАВС = АВ + ВС + АС
Так как АВ = АС, то РΔАВС = 2АВ + ВС = 32 (см)
2АВ + ВС = 32
2(АВ + 1/2ВС) = 32
АВ + 1/2ВС = 32 : 2
АВ + 1/2ВС = 16
РΔАВМ = АВ + ВМ + АМ
Так как АМ — медиана, то ВМ = МС = 1/2ВС, тогда РΔАВМ = АВ + 1/2ВС + АМ = 24 (см)
Но АВ + 1/2ВС = 16, тогда:
АВ + 1/2ВС + АМ = 24
16 + АМ = 24
АМ = 24 — 16
АМ = 8 (см)
О т в е т: АМ = 8 см.
110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольник равнобедренный.

Д а н о
ΔАВС
АМ — медиана и высота
Д о к а з а т ь
ΔАВС — равнобедренный
Д о к а з а т е л ь с т в о
Так как АМ — медиана, то ВМ = МС.
Так как АМ — высота, то ∠ВМА = ∠АМС = 90°.
АМ ∈ ΔАВМ, АМ ∈ ΔАМС, следовательно, АМ — общая сторона для ΔАВМ и ΔАМС. Тогда ΔАВМ = ΔАМС по первому признаку равенства треугольников (по двум сторонам и углу между ними).
У равных треугольников соответствующие стороны и углы равны, то есть АВ = АС и ΔАВС — равнобедренный, ЧТД (что и требовалось доказать).
О т в е т: ΔАВС — равнобедренный.
111. На рисунке 65 CD = BD, ∠1 = ∠2. Докажите, что треугольник ABC равнобедренный.
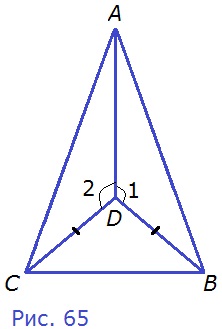
Д а н о
CD = BD
∠1 = ∠2
Д о к а з а т ь
ΔАВС — равнобедренный
Д о к а з а т е л ь с т в о
АD ∈ ΔАCD, АD ∈ ΔАDB, следовательно, АD — общая сторона для ΔАCD и ΔАDB. CD = BD и ∠1 = ∠2 — по условию. Тогда ΔАCD = ΔАDB по первому признаку равенства треугольников (по двум сторонам и углу между ними).
У равных треугольников соответствующие стороны и углы равны, то есть АC = АB и ΔАВС — равнобедренный, ЧТД (что и требовалось доказать).
О т в е т: ΔАВС — равнобедренный.
| ← Предыдущая | Следующая → |