Обыкновенные дроби
Сравнение дробей
Ответы к стр. 182
804. а) Как сравнивают дроби с общим знаменателем?
б) Как сравнивают дроби с разными знаменателями?
а) Из двух дробей с общим знаменателем больше та дробь, у которой числитель больше.
б) Чтобы сравнить две дроби с разными знаменателями, их нужно привести к общему знаменателю, а затем применить правило сравнения дробей с общим знаменателем.
805. а) Какую дробь называют правильной?
б) Какую дробь называют неправильной?
а) Дробь называется правильной, если её числитель меньше знаменателя.
б) Дробь называется неправильной, если её числитель больше знаменателя или равен ему.
806. Сравните:
а) правильную дробь с 1; б) неправильную дробь с 1; в) правильную дробь с неправильной.
а) Правильная дробь всегда меньше 1.
б) Неправильная дробь больше или равна 1.
в) Правильная дробь всегда меньше неправильной.
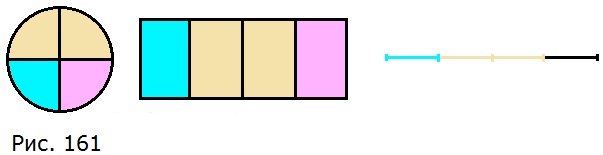
807. С помощью рисунка 161 объясните, почему 3⁄4 > 1⁄4, 1⁄2 < 3⁄4.
Каждый рисунок разделен на 4 части. Каждая часть представляет собой 1⁄4 часть фигуры. Если взять 3 таких части, то получим 3⁄4 часть фигуры. 3 > 1, поэтому 3⁄4 > 1⁄4.
Если взять 2 таких части, то получим 2⁄4 части фигуры или половину фигуры, значит 2⁄4 = 1⁄2. 2 < 3, поэтому 2⁄4 < 3⁄4, 1⁄2 < 3⁄4.
808. Постройте отрезок AB = 12 см. Отметьте на AB точку C так, чтобы:
а) AC = 1⁄4 AB; б) AC = 1⁄6 AB.
Сравните длины отрезков AB и AC, BC и AC, BC и AB.
а) AC = 1⁄4 AB = 12 : 4 = 3 (см)
AC = 1⁄4 AB
BC = 3⁄4 AB
AC < AB
AC < BC
BC < AB
б) AC = 1⁄6 AB = 12 : 6 = 2 (см)
AC = 1⁄6 AB
BC = 5⁄6 AB
AC < AB
AC < BC
BC < AB
809. Сравните дроби и результат сравнения запишите с помощь знаков > и <:
а) 1⁄5 и 4⁄5; б) 2⁄7 и 1⁄7; в) 7⁄15 и 8⁄15;
г) 7⁄81 и 6⁄81; д) 27⁄100 и 33⁄100; е) 1700⁄1995 и 1800⁄1995.
а) 1⁄5 < 4⁄5;
б) 2⁄7 > 1⁄7;
в) 7⁄15 < 8⁄15;
г) 7⁄81 > 6⁄81;
д) 27⁄100 < 33⁄100;
е) 1700⁄1995 < 1800⁄1995.
810. Сравните дроби и результат сравнения запишите с помощь знаков = и ≠:
а) 3⁄5 и 16⁄10; б) 2⁄3 и 16⁄21; в) 7⁄5 и 27⁄20;
г) 1⁄2 и 50⁄100; д) 1⁄4 и 25⁄100; е) 3⁄4 и 75⁄100.
а) НОК (5, 10) = 10
3⁄5 = 3•2⁄5•2 = 6⁄10
6⁄10 ≠ 16⁄10, значит: 3⁄5 ≠ 16⁄10
б) НОК (3,21) = 21
2⁄3 = 2•7⁄3•7 = 14⁄21
14⁄21 ≠ 16⁄21, значит: 2⁄3 ≠ 16⁄21
в) НОК (5,20) = 20
7⁄5 = 7•4⁄5•4 = 28⁄20
28⁄20 ≠ 27⁄20, значит: 7⁄5 ≠ 27⁄20
г) НОК (2,100) = 100
1⁄2 = 1•50⁄2•50 = 50⁄100
50⁄100 = 50⁄100, значит: 1⁄2 = 50⁄100
д) НОК (4,100) = 100
1⁄4 = 1•25⁄4•25 = 25⁄100
25⁄100 = 25⁄100, значит: 1⁄4 = 25⁄100
е) НОК (4,100) = 100
3⁄4 = 3•25⁄4•25 = 75⁄100
75⁄100 = 75⁄100, значит: 3⁄4 = 75⁄100
811. а) Что тяжелее: 3⁄8 конфет или 7⁄20 кг печенья?
б) Что тяжелее: 1⁄2 пуха или 9⁄18 кг железа?
а) НОК (8, 20) = 40
3⁄8 = 3•5⁄8•5 = 15⁄40
7⁄20 = 7•2⁄20•2 = 14⁄40
15⁄40 > 14⁄40, значит: 3⁄8 > 7⁄20
Ответ: 3⁄8 конфет тяжелее, чем 7⁄20 кг печенья.
б) НОК (2, 18) = 18
1⁄2 = 1•9⁄2•9 = 9⁄18
9⁄18 = 9⁄18, значит: 1⁄2 = 9⁄18
Ответ: 1⁄2 пуха весят столько же, сколько 9⁄18 кг железа.
812. Сравните дроби с одинаковыми числителями:
а) 1⁄2 и 1⁄3; б) 1⁄7 и 1⁄4; в) 2⁄5 и 2⁄3;
г) 3⁄5 и 3⁄7; д) 7⁄13 и 7⁄15; е) 8⁄7 и 8⁄11.
а) НОК (2, 3) = 6
1⁄2 = 1•3⁄2•3 = 3⁄6
1⁄3 = 1•2⁄3•2 = 2⁄6
3⁄6 > 2⁄6, значит: 1⁄2 > 1⁄3, следовательно, из двух дробей с равными числителями больше та дробь, у которой знаменатель меньше
б) 1⁄7 < 1⁄4
в) 2⁄5 < 2⁄3
г) 3⁄5 >3⁄7
д) 7⁄13 > 7⁄15
е) 8⁄7 > 8⁄11
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.