Натуральные числа и нуль
Занимательные задачи
Ответы к стр. 74
321. Из точки A, показанной на схеме города, надо попасть в точку B, двигаясь только вправо и вверх. На рисунке 34, а показан один из маршрутов движения. Убедитесь, что это можно сделать только 6 способами.
Р е ш е н и е. Чтобы убедиться, что различных маршрутов движения от А к В только 6, можно их нарисовать по отдельности. Мы поступим проще. Укажем в каждой точке, в которой можно изменить направление движения, число способов, которыми можно прийти в эту точку (рис. 34, б). В точку В можно прийти 3 + 3 = 6 способами.
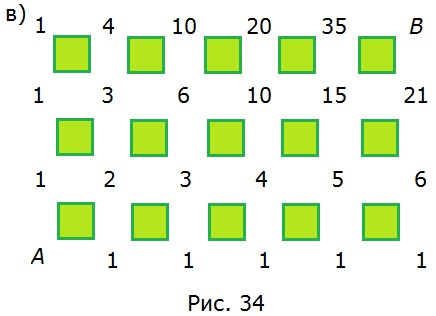
322. Если мы захотим показать все маршруты движения (только вправо и вверх) из A в B (рис. 34, в), то придется много потрудиться. Гораздо проще подсчитать их число описанным выше способом. Подсчитайте.
В точку В можно прийти 35 + 21 = 56 способами.
323. Коля написал два раза свое имя (рис. 35, а). Его сосед по парте заметил, что Коля может прочитать свое имя более, чем 10 способами, и показал один из них (рис. 35, б). Сколькими способами Коля может прочитать свое имя?
а) К О Л Я
К О Л Я
б) К — О Л Я
\
К О Л — Я
Рис. 35
Посчитаем количество способов, которыми можно пройти каждую букву, и запишем это число рядом с буквой.
К1 О2 Л4 Я8
К1 О2 Л4 Я8
Получается 8 + 8 = 16 способа прочитать имя.
О т в е т: 16 способов.
324. На рисунке 36 показано, как можно прочитать слово «МАРШРУТ». Подсчитайте число всех способов, которыми можно прочитать это слово.
М Р Р Т
\ / \ /
А Ш У
\ /
М Р Р Т
А Ш У
М Р Р Т
Рис. 36
Посчитаем количество способов, которыми можно пройти каждую букву, и запишем это число рядом с буквой.
М Р2 Р6 Т18
А2 Ш6 У18
М Р4 Р12 Т36
А2 Ш6 У18
М Р2 Р6 Т18
Получается 18 + 36 + 18 = 72 способа прочитать слово.
О т в е т: 72 способа.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.