Натуральные числа
Сложение и вычитание натуральных чисел
Буквенная запись свойств сложения и вычитания
Ответы к стр. 55
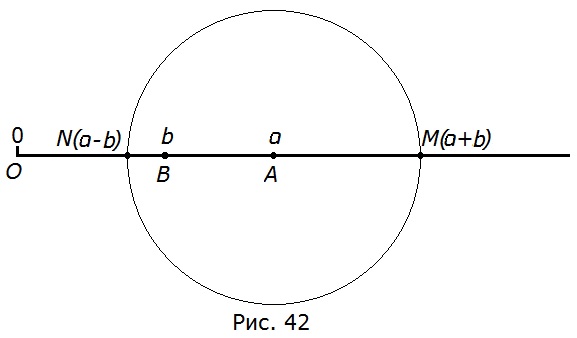
340. а) На рисунке 42 с помощью циркуля найдите точки М(α + b) и N (α — b).
б) Объясните по рисунку 43 смысл сочетательного свойства сложения.
Чтобы прибавить к числу сумму двух чисел (b + c), можно сначала прибавить первое слагаемое b, а потом к полученной сумме — второе слагаемое c.
в) Объясните с помощью рисунков остальные свойства сложения и вычитания.
1) Сумма чисел не меняется при перестановке слагаемых: α + b = b + α.
2) От прибавления нуля число не изменяется: α + 0 = α.
3) Для того, чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности — второе слагаемое: α — (b + c) = α — b — c.
4) Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое: (α + b) — c = α — c + b.
5) Если из числа вычесть это число — получистся нуль, если из числа вычесть нуль — оно не изменится.
341. Из свойств сложения следует:
56 + х + 14 = х + 56 + 14 = х + (56 + 14) = х + 70.
По этому образцу упростите выражение:
а) 23 + 49 + m; в) х + 54 + 27;
б) 38 + n + 27; г) 176 + у + 24.
а) 23 + 49 + m (23 + 49) + m = 72 + m;
б) 38 + n + 27 = n + 38 + 27 = n + (38 + 27) = n + 65;
в) х + 54 + 27 = x + (54 + 27) = x + 81;
г) 176 + у + 24 = у + 176 + 24 = у + (176 + 24) = у + 200.
342. Найдите значение выражения, предварительно упростив его:
а) 28 + m + 72 при m = 87; в) 228 + k + 272 при k = 48;
б) n + 49 + 151 при n = 63; г) 349 + р + 461 при р = 115.
а) 28 + m + 72 = m + 28 + 72 = m + (28 + 72) = m + 100, при m = 87: 87 + 100 = 187;
б) n + 49 + 151 = n + (49 + 151) = n + 200, при n = 63: 63 + 200 = 263;
в) 228 + k + 272 = k + 228 + 272 = k + (228 + 272) = k + 500, при k = 48: 48 + 500 = 548;
г) 349 + р + 461 = р + 349 + 461 = р + (349 + 461) = р + 810, при р = 115: 115 + 810 = 925.
343. Из свойств вычитания следует:
28 — (15 + с) = 28 — 15 — с = 13 — с,
α — 64 — 26 = α — (64 + 26) = α — 90.
Какое свойство вычитания применено в этих примерах? Используя это свойство вычитания, упростите выражение:
а) 35 — (18 + у); б) m — 128 — 472.
Свойство вычитания суммы из числа.
а) 35 — (18 + у) = 35 — 18 — у = 17 — у;
б) m — 128 — 472 = m — (128 + 472) = m — 600.
344. Из свойств сложения и вычитания следует:
137 — с — 27 = 137 — (с + 27) = 137 — (27 + с) = 137 — 27 — с = 110 — с.
Какие свойства сложения и вычитания применены в этом примере? Используя эти свойства, упростите выражение:
а) 168 — (х + 47);
б) 384 — m — 137.
Свойство вычитания суммы из числа и переместительное свойство сложения.
а) 168 — (х + 47) = 168 — (47 + х) = 168 — 47 — х = 121 — х;
б) 384 — m — 137 = 384 — (m + 137) = 384 — (137 + m) = 384 — 137 — m = 247 — m.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И