Отношения, пропорции, проценты
Занимательные задачи
Ответы к стр. 43
185. 2 землекопа за 2 ч выкопают 2 м канавы. Сколько землекопов за 5 ч выкопают 5 м канавы?
1) 2 (м) : 2 (ч) = 1 (м) — выкопают 2 землекопа за 1 час
2) 1 (м) : 2 (землекопа) = 1/2 (м) — выкопает 1 землекоп за 1 час
3) 1/2 (м) • 5 (ч) = 2 1/2 (м) — выкопает 1 землекоп за 5 часов
4) 5 (м) : 2 1/2 (м) = 5 : 5/2 = 5 • 2/5 = 10/5 = 2 (землекопа) — выкопаю 5 метров канавы за 5 часов
О т в е т: 2 землекопа.
186. Из «Всеобщей арифметики» И. Ньютона. Если писец может за 8 дней написать 15 листов, сколько понадобится писцов, чтобы написать 405 листов за 9 дней?
1) 15 (листов) : 8 (дней) = 15/8 (листов) — напишет 1 писец за 1 день
2) 15/8 (листов) • 9 (дней) = 135/8 (листов) — напишет 1 писец за 9 дней
3) 405 (листов) : 135/8 (листов) = 405 • 8/135 = 3 • 8 = 24 (писца) — напишут 405 листов за 9 дней
О т в е т: 24 писца.
187. Переписчик в течение 4 дней может переписать 40 листов, работая по 9 ч в день. Во сколько дней он перепишет 60 листов, работая по 12 ч в день?
1) 40 (листов) : 4 (дня) = 10 (листов) — переписчик перепишет за один 9-ти часовой рабочий день
2) 10 (листов) : 9 (часов) = 10/9 (листов) — перепишет переписчик за 1 час
3) 10/9 (листов) • 12 (часов) = 40/3 (листов) — перепишет переписчик за 12-и часовой рабочий день
4) 60 (листов) : 40/3 (листов) = 60 • 3/40 = 9/2 = 4 1/2 (дня) — 12-и часовых рабочих дня потребуется переписчику чтобы переписать 60 листов
О т в е т: 4 1/2 дня.
188. У хозяйки спросили: «Хорошо ли несутся ваши куры?» − «Считайте сами, − был ответ, − полторы курицы за полтора дня несут полтора яйца, а всего у меня 12 кур». Сколько яиц несут куры в день?
Полтора — это 1 1/2
1) 1 1/2 (яйца) : 1 1/2 (курицы) = 1 (яйцо) — сносит 1 курица за полтора дня
2) 1 яйцо : 1 1/2 дня = 1 : 3/2 = 1 • 2/3 = 2/3 (яйца) — сносит 1 курица за 1 день
3) 2/3 (яйца) • 12 (куриц) = 2 • 4 = 8 (яиц) — снесут 12 куриц за 1 день
О т в е т: 8 яиц.
189. Зарплата в 100 условных единиц, повысилась на 10 %, потом еще на 10 %. На сколько процентов повысилась зарплата за 2 раза?
10 % — это 1/10 числа
1) 100 + 100 • 1/10 = 100 + 100/10 = 100 + 10 = 110 (условных единиц) — составила заработная плата после первого повышения
2) 110 + 110 • 1/10 = 110 + 110/10 = 110 + 11 = 121 (условных единиц) — составила заработная плата после второго повышения
3) 121/100 • 100 % — 100 % = 121 % — 100 % = 21 % — повысилась заработная плата после двух повышений
О т в е т: на 21 %.
190. Цена товара в 100 условных единиц, понизилась на 10 %, потом еще на 10 %. На сколько процентов понизилась цена товара за 2 раза?
10 % − это 1/10 числа
1) 100 — 100 • 1/10 = 100 — 100/10 = 100 — 10 = 90 (условных единиц) — составила цена после первого понижения
2) 90 — 90 • 1/10 = 90 — 90/10 = 90 — 9 = 81 (условных единиц) — составила цена после второго понижения
3) 100 % — 81/100 • 100 % = 100 % — 81 % = 19 % — понизилась цена после двух понижений
О т в е т: на 19 %.
191. Цена товара в 100 условных единиц сначала понизилась на 10 %, потом повысилась на 10 %. На сколько процентов понизилась или повысилась цена товара за 2 раза?
10 % — это 1/10 числа
1) 100 — 100 • 1/10 = 100 — 100/10 = 100 — 10 = 90 (условных единиц) — составила цена после понижения
2) 90 + 90 • 1/10 = 90 + 90/10 = 90 + 9 = 99 (условных единиц) — составила цена после повышения
3) 100 % — 99/100 • 100 % = 100 % — 99 % = 1 % — понизилась цена после двух изменений
О т в е т: на 1 % понизилась.
192. Цена товара в 100 условных единиц сначала повысилась на 10 %, потом понизилась на 10 %. На сколько процентов понизилась или повысилась цена товара за 2 раза?
10 % − это 1/10 числа
1) 100 + 100 • 1/10 = 100 + 100/10 = 100 + 10 = 110 (условных единиц) — составила цена после повышения
2) 110 — 110 • 1/10 = 110 — 110/10 = 110 — 11 = 99 (условных единиц) — составила цена после понижения
3) 100 % — 99/100 • 100 % = 100 % — 99 % = 1 % — понизилась цена после двух изменений
О т в е т: на 1 % понизилась.
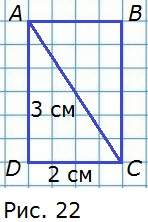
193. Известно, что площади равных фигур равны и площадь фигуры равна сумме площадей составляющих её частей. Вычислите площадь (рис. 22): а) прямоугольника ABCD; б) треугольника ABC; в) треугольника ADC.
Площадь прямоугольника равна произведению его сторон: SABCD = 2 см • 3 см = 6 см2.
Площадь прямоугольника ABCD = площадь треугольника ABC + площадь треугольника ADC. Треугольники ABC и ADC равны.
6 см2 : 2 = 3 см2 — площадь треугольника ABC;
6 см2 : 2 = 3 см2 — площадь треугольника ADC.
194. Вычислите площадь многоугольника (длины сторон в сантиметрах указаны на рисунке 23).
а) 5 • 5 + (6 + 5) • 3 = 25 + 33 = 58 (см2);
б) 10 • 6 — 2 • 4 = 60 — 8 = 52 (см2).
| ← Предыдущая | Следующая → |
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.