Алгебраические выражения
Формулы сокращённого умножения
Разность квадратов
Ответы к стр. 108
376. Представьте выражение в виде многочлена двумя способами:
а) (p + q)(p − q); б) (α − b)(α + b); в) (c + d)(d − c);
г) (y − x)(x + y); д) (α − 3)(3 + α); е) (2 − b)(b + 2);
ж) (m + 1)(m − 1); з) (7 − n)(7 + n).
а) (p + q)(p − q) = p2 + pq – pq − q2 = p2 − q2,
(p + q)(p − q) = p2 − q2;
б) (α − b)(α + b) = α2 – αb + αb − b2 = α2 − b2,
(α − b)(α + b) = α2 − b2;
в) (c + d)(d − c) = (d + c)(d − c) = d2 + cd – cd − c2 = d2 − c2,
(c + d)(d − c) = (d + c)(d − c) = d2 − c2;
г) (y − x)(x + y) = (y − x)(y + x) = y2 – xy + xy − x2 = y2 − x2,
(y − x)(x + y) = (y − x)(y + x) = y2 − x2;
д) (α − 3)(3 + α) = (α − 3)(α + 3) = α2 − 3α + 3α – 9 = α2 − 9,
(α − 3)(3 + α) = (α − 3)(α + 3) = α2 − 9;
е) (2 − b)(b + 2) = (2 − b)(2 + b) = 4 − 2b + 2b − b2 = 4 − b2,
(2 − b)(b + 2) = (2 − b)(2 + b) = 4 − b2;
ж) (m + 1)(m − 1) = m2 + m – m – 1 = m2 − 1,
(m + 1)(m − 1) = m2 − 1;
з) (7 − n)(7 + n) = 49 − 7n + 7n − n2 = 49 − n2,
(7 − n)(7 + n) = 49 − n2.
377. Упростите выражение, используя формулу разности квадратов. Сначала представьте выражение в виде разности квадратов, затем упростите запись степени.
Например: (3α − 2b)(3α + 2b) = (3α)2 − (2b)2 = 9α2 − 4b2.
а) (x + 2y)(x − 2y); б) (2α + b)(2α − b);
в) (3m − n)(3m + n); г) (p − 7q)(7q + p);
д) (2α − 3b)(2α + 3b); е) (5x + 4y)(4y − 5x);
ж) (4p − 1)(1 + 4p); з) (5m + 8n)(8n − 5m);
и) (4y − 7x)(7x + 4y); к) (11α − 13b)(11α + 13b).
а) (x + 2y)(x − 2y) = x2 − (2y)2 = x2 − 4y2;
б) (2α + b)(2α − b) = (2α)2 − b2 = 4α2 − b2;
в) (3m − n)(3m + n) = (3m)2 − n2 = 9m2 − n2;
г) (p − 7q)(7q + p) = (p − 7q)(p − 7q) = p2 − (7q)2 = p2 − 49q2;
д) (2α − 3b)(2α + 3b) = (2α)2 − (3b)2 = 4α2 − 9b2;
е) (5x + 4y)(4y − 5x) = (4y + 5x)(4y − 5x) = (4y)2 − (5x)2 = 16y2 − 25x2;
ж) (4p − 1)(1 + 4p) = (4p − 1)(4p + 1) = (4p)2 – 12 = 16p2 − 1;
з) (5m + 8n)(8n − 5m) = (8n + 5m)(8n − 5m) = (8n)2 − (5m)2 = 64n2 − 25m2;
и) (4y − 7x)(7x + 4y) = (4y − 7x)(4y + 7x) = (4y)2 − (7x)2 = 16y2 − 49x2;
к) (11α − 13b)(11α + 13b) = (11α)2 − (13b)2 = 121α2 − 169b2.
378. Вычислите, используя формулу разности квадратов:
а) 71 • 69; б) 82 • 78; в) 299 • 301;
г) 498 • 502; д) 3,01 • 2,99; е) 10,2 • 9,8.
а) 71•69 = (70 + 1)(70 − 1) = 702 – 12 = 4900 – 1 = 4899;
б) 82•78 = (80 + 2)(80 − 2) = 802 – 22 = 6400 – 4 = 6396;
в) 299•301 = (300 − 1)(300 + 1) = 3002 – 12 = 90 000 – 1 = 89 999;
г) 498•502 = (500 − 2)(500 + 2) = 5002 – 22 = 250 000 – 4 = 249 996;
д) 3,01•2,99 = (3 + 0,01)(3 − 0,01) = 32 − 0,012 = 9 − 0,0001 = 8,9999;
е) 10,2•9,8 = (10 + 0,2)(10 − 0,2) = 102 − 0,22 = 100 − 0,04 = 99,96.
379. Представьте выражение в виде квадрата:
а) 121; б) x4; в) α6; г) 4x2y6;
д) 25m2n6; е) 1/4 p2; ж) 0,25x4; з) 21/4 x4q2.
а) 121 = 112;
б) x4 = (x2)2;
в) α6 = (α3)2;
г) 4x2y6 = (2xy3)2;
д) 25m2n6 = (5mn3)2;
е) 1/4 p2 = (1/2 p)2;
ж) 0,25x4 = (0,5x2)2;
з) 21/4 x4q2 = 9/4 x4q2 = (3/2 x2q)2 = (11/2 x2q)2.
380. Представьте выражение в виде разности квадратов:
a) x4 — 1; б) 4α2 — 4; в) m6 — 25;
г) 16у2 — 49x2; д) 9р4 — 16q6; е) З6m2 — 16n2.
а) x4 — 1 = (x2)2 − 12;
б) 4α2 — 4 = (2α)2 − 22;
в) m6 — 25 = (m3)2 − 52;
г) 16у2 — 49x2 = (4y)2 − (7x)2;
д) 9р4 — 16q6 = (3p2)2 − (4q3)2;
е) З6m2 — 16n2 = (6m)2 − (4n)2.
Разложите многочлен на множители (381-382):
381. а) α2 — b2; б) y2 — x2;
в) (2x)2 — 1; г) 9 — (Зm)2;
д) 16 — р4; е) 25 — α6;
ж) m4 — n2; з) p8 — 49;
и) 1 — x4; к) α4 — b4.
а) α2 — b2 = (α − b)(α + b);
б) y2 — x2 = (y − x)(y + x);
в) (2x)2 – 1 = (2x − 1)(2x + 1);
г) 9 — (Зm)2 = 32 − (3m)2 = (3 − 3m)(3 + 3m) = 3(1 − m)3(1 + m) = 9(1 − m)(1 + m);
д) 16 — р4 = 42 − (p2)2 = (4 − p2)(4 + p2) = (22 − p2)(4 + p2) = (2 − p)(2 + p)(4 + p2);
е) 25 — α6 = 52 − (α3)2 = (5 − α3)(5 + α3);
ж) m4 — n2 = (m2)2 − n2 = (m2 − n)(m2 + n);
з) p8 – 49 = (p4)2 – 72 = (p4 − 7)(p4 + 7);
и) 1 — x4 = 12 − (x2)2 = (1 − x2)(1 + x2) = (1 − x)(1 + x)(1 + x2);
к) α4 — b4 = (α2)2 − (b2)2 = (α2 − b2)(α2 + b2) = (α − b)(α + b)(α2 + b2).
382. а) 4α2 — 1; б) 4α2 — 9b2;
в) 9х4 — 4; г) x4 — 16.
а) 4α2 – 1 = (2α)2 – 12 = (2α − 1)(2α + 1);
б) 4α2 − 9b2 = (2α)2 − (3b)2 = (2α − 3b)(2α + 3b);
в) 9x4 – 4 = (3x2)2 – 22 = (3x2 − 2)(3x2 + 2);
г) x4 – 16 = (x2)2 – 42 = (x2 − 4)(x2 + 4) = (x2 − 22)(x2 + 4) = (x2 − 2)(x2 + 2)(x2 + 4).
383. Доказываем. Пользуясь рисунком 15, докажите формулу разности квадратов для α > 0, b > 0, α > b.
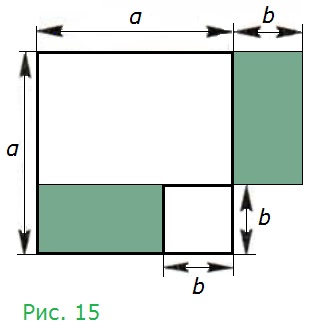
α • α = α2 − площадь большого квадрата
b • b = b2 − площадь малого квадрата
(α − b)b − площадь каждого из двух закрашенных прямоугольников
Тогда:
α2 = (α – b)α + b2 + (α − b)b
α2 – b2 = (α – b)α + (α − b)b
α2 – b2 = (α – b)(α + b).
384. Вместо букв С и D подберите одночлены так, чтобы выполнялось равенство:
а) (2α — С) (2α + b2) = 4α2 — b4;
б) (С + D)(x2 — у) = х4 — у2;
в) (Зm — С)(D + 2n) = 9m2 — 4n2;
г) (С + 5q)(5q + D) = 25q2 — 16р4.
*В примере г) опечатка – в одной из скобок должен быть знак «-».
а) (2α − C)(2α + b2) = 4α2 − b4
C2 = b4
C2 = (b2)2
C = b2
б) (C + D)(x2 − y) = x4 − y2
C2 = x4 D2 = y2
C2 = (x2)2 D = y
C = x2
в) (3m − C)(D + 2n) = 9m2 − 4n2
C2 = 4n2 D2 = 9m2
C2 = (2n)2 D2 = (3m)2
C = 2n D = 3m
г) (C — 5q)(5q + D) = 25q2 − 16p4
(C — 5q)(D + 5q) = 25q2 − 16p4
C2 = D2 = 16p4
C2 = D2 = (4p2)2
C = D = 4p2
| ← Предыдущая | Следующая → |