Алгебраические выражения
Многочлены
Произведение одночлена и многочлена
Ответы к стр. 86
276. а) По какому правилу умножают одночлен на многочлен?
б) Какие многочлены называют противоположными?
в) Каким свойством обладают противоположные многочлены?
г) Каким свойством обладает разность многочленов?
д) Изменится ли многочлен, если его умножить на 1?
а) Чтобы умножить одночлен на многочлен, нужно одночлен умножить на каждый член многочлена и результат записать в виде многочлена.
б) Данный многочлен и многочлен, полученный умножением его на число −1, называют противоположными многочленами.
в) Сумма противоположных многочленов равна нулю.
г) Разность двух многочленов есть сумма уменьшаемого и многочлена, противоположного вычитаемому.
д) Если многочлен умножить на 1, то он не изменится.
Найдите многочлен, равный произведению одночлена и многочлена (277 – 279):
277. а) 3 и (α + b); б) x и (α − b); в) (x + 1) и 5; г) (α − b) и x.
а) 3(α + b) = 3α + 3b;
б) x(α — b) = xα – xb;
в) (x + 1) • 5 = 5x + 5;
г) (α — b) • x = αx – bx.
278. а) (α + 3)7; б) (x − y)10; в) α(x − y);
г) α(α + b); д) (α + b − c)2; е) (α − b)(−6).
а) (α + 3)7 = 7α + 21;
б) (x − y)10 = 10x − 10y;
в) α(x − y) = αx – αy;
г) α(α + b) = αα + αb = α2 + αb;
д) (α + b − c)2 = 2α + 2b − 2c;
е) (α − b)(−6) = -6α + 6b.
279. а) (−2)(x + y); б) (7 + 3y − x2y)(−2xy);
в) 3αb(α2 − 2α + 1); г) 2α(x + y);
д) (x2 + 2xy + y2)(−12xy3); е) 21α2b5(α3 − 4αb2 − b2);
ж) (−αbc)(αb + αc + bc); з) −αc(α + 2c).
а) (−2)(x + y) = −2x − 2y;
б) (7 + 3y − x2y)(−2xy) = −14xy − 6xy2 + 2x3y2;
в) 3αb(α2 − 2α + 1)= 3α3b − 6α2b + 3αb;
г) 2α(x + y) = 2αx + 2αy;
д) (x2 + 2xy + y2)(−12xy3) = −12x3y3 − 24x2y4 − 12xy5;
е) 21α2b5(α3 − 4αb2 − b2) = 21α5b5 − 84α3b7 − 21α2b7;
ж) (−αbc)(αb + αc + bc) = −α2b2c − α2bc2 − αb2c2;
з) −αc(α + 2c) = −α2c−2αc2.
Преобразуйте выражение в многочлен стандартного вида (280 – 281):
280. а) 2(α + b) + 4(α + b); б) 4(x − y) + 7(x − y);
в) 4 − 2(x + 1); г) 2α − 3(b − α);
д) 2(α − b) − 3(α + b); е) α(x − y) − b(x + y);
ж) 3α2 − α(3α − 4b) − 2(b − 4α); з) 2αb(α + 2b) − 3αb2(α − 4).
а) 2(α + b) + 4(α + b) = 2α + 2b + 4α + 4b = 6α + 6b;
б) 4(x − y) + 7(x − y) = 4x − 4y + 7x − 7y = 11x − 11y;
в) 4 − 2(x + 1) = 4 − 2x − 2 = −2x + 2;
г) 2α − 3(b − α) = 2α − 3b + 3α = 5α − 3b;
д) 2(α − b) − 3(α + b) = 2α − 2b − 3α — 3b = −α − 5b;
е) α(x − y) − b(x + y) = αx − αy − bx – by;
ж) 3α2 − α(3α − 4b) − 2(b − 4α) = 3α2 − 3α2 + 4αb − 2b + 8α = 8α + 4αb − 2b;
з) 2αb(α + 2b) − 3αb2(α − 4) = 2α2b + 4αb2 − 3α2b2 + 12αb2 = 2α2b − 3α2b2 + 16αb2.
281. а) α(b − c) + b(c − α) + c(α − b);
б) α(b + c − bc) − b(c + α − αc) + c(b − α).
а) α(b − c) + b(c − α) + c(α − b) = αb − αc + bc − αb + αc − bc = 0;
б) α(b + c − bc) − b(c + α − αc) + c(b − α) = αb + αc − αbc − bc − αb + αbc = 0.
282. Доказываем. Пользуясь рисунком 11, докажите, что для α > 0, b > 0, c > 0, d > 0 верно равенство:
а) α(b + c) = αb + αc (рис. 11, а);
б) α(b + c + d) = αb + αc + αd (рис. 11, б).
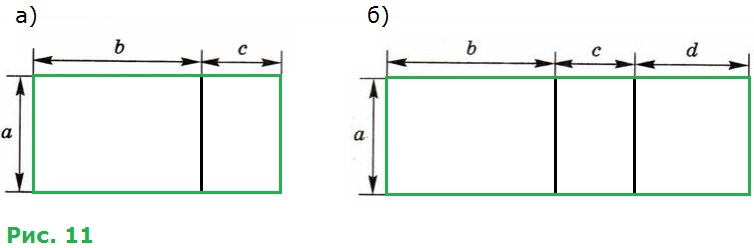
а) Площадь всего прямоугольника равна сумме площадей входящих в него прямоугольников.
α(b + c) − площадь всего прямоугольника, αb − площадь левого прямоугольника, αc − площадь правого прямоугольника, тогда:
α(b + c) = αb + αc.
б) Площадь всего прямоугольника равна сумме площадей входящих в него прямоугольников.
α(b + c + d) − площадь всего прямоугольника, αb − площадь левого прямоугольника, αc − площадь среднего прямоугольника, αd − площадь правого прямоугольника, тогда:
α(b + c + d) = αb + αc + αd.
| ← Предыдущая | Следующая → |