Начальные геометрические сведения
Сравнение отрезков и углов
Равенство геометрических фигур. Сравнение отрезков и углов
Ответы к стр. 13
21. Луч ОС делит угол АОВ на два угла. Сравните углы АОВ и АОС.
Луч ОС проходит внутри ∠АОВ и делит его на ∠АОС и ∠СОВ, причём ∠АОВ = ∠АОС + ∠СОВ. Следовательно, ∠АОС составляет часть ∠АОВ и ∠АОВ > ∠АОС.
22. Луч I — биссектриса угла hk. Можно ли наложением совместить углы: а) hl и Ik; б) hl и hk?
а) луч l — биссектриса и делит ∠hk на два равных угла, то есть ∠hk = ∠hl + ∠lk и ∠hl = ∠lk, следовательно, ∠hl и ∠lk при наложении совместятся;
б) луч l — биссектриса и делит ∠hk на два равных угла, то есть ∠hk = ∠hl + ∠lk и ∠hl составляет часть ∠hk, следовательно, ∠hl и ∠hk при наложении не совместятся.
23. На рисунке 26 углы, обозначенные цифрами, равны. Укажите: а) биссектрису каждого из углов АОС, BOF, АОЕ; б) все углы, биссектрисой которых является луч ОС.
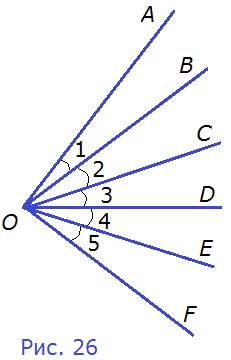
а) ∠АОС = ∠АОВ + ∠ВОС, ∠АОВ = ∠ВОС, следовательно, луч ОВ — биссектриса ∠АОС;
∠ВОF = ∠BOD + ∠DOF, ∠BOD = ∠ВOC + ∠СOD, ∠DOF = ∠DOE + ∠ЕOF, ∠ВOC + ∠СOD = ∠DOE + ∠ЕOF или ∠BOD = ∠DOF, следовательно, луч ОD — биссектриса ∠BОF;
∠AОE = ∠AOC + ∠COE, ∠AOC = ∠AOB + ∠BOC, ∠COE = ∠COD + ∠DOE, ∠AOB + ∠BOC = ∠COD + ∠DOE или ∠AOC = ∠COE, следовательно, луч ОC — биссектриса ∠AОE;
б) луч ОС является стороной ∠ВОС и ∠СОD, ∠ВОС = ∠СОD, ∠ВОС + ∠СОD = ∠ВОD, следовательно, луч ОС является биссектрисой ∠ВОD;
луч ОС является стороной ∠AОС и ∠СОE, ∠AOC = ∠AOB + ∠BOC, ∠COE = ∠COD + ∠DOE, ∠AOB + ∠BOC = ∠COD + ∠DOE или ∠AOC = ∠COE, ∠AOC + ∠COE = ∠AОE, следовательно, луч ОС является биссектрисой ∠AОE.
| ← Предыдущая | Следующая → |